P2163 [SHOI2007]园丁的烦恼

题目描述：

二维平面有n个坐标，每个坐标都表示该点处有一颗树苗，进行m次询问，每次询问给出两个坐标，表示一个矩形的左下角和右上角，输出这个矩形中的树苗的数量，包括矩形的边界

思路：

二维偏序天花板

二维偏序 + 容斥 + 离散化 + 树状数组 + 思维

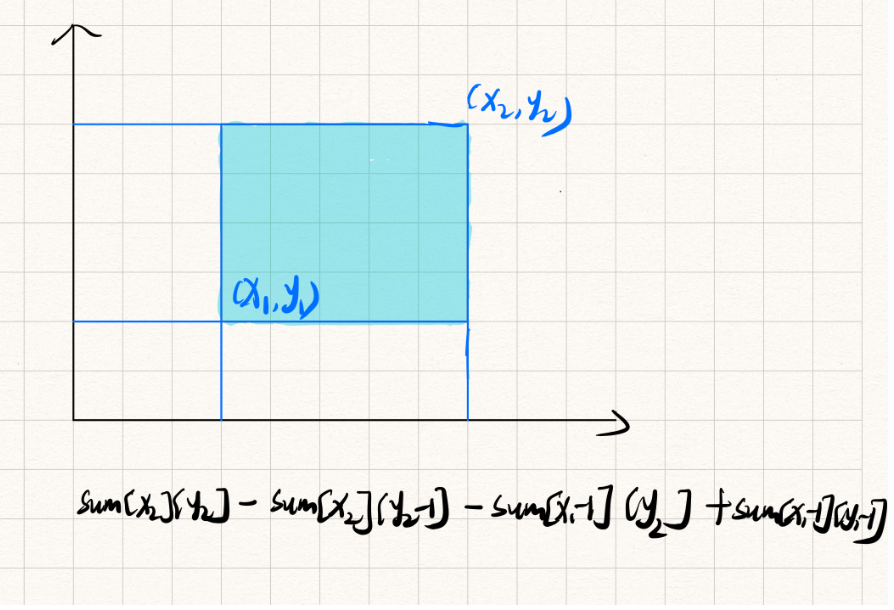
做过前几个二维偏序的题后，这个题的思路就非常简单，其实就是求满足 $x1<=x_i<=x2, y1<=y_i<=y2$ 的 $(x_i,y_i)$的数量，其中 $(x_i, y_i)$是输入的n个树苗的点， $(x1, y1), (x2,y2)$是询问矩形的左下角和右上角，很容易的就可以联想到用前缀和来处理，但是因为是二维的，所以是需要容斥的，和二维前缀和的容斥一样，如下：

这样其实就近似转换成求满足 $xi<=x_j, y_i <= y_j，(i <= j)$ 的 (i,j)的数量，那这不就是二维偏序了吗，由于这个n个点的坐标和这m次询问的坐标并不会完全重合，所以我们需要存下所有的询问，离线处理

我第一遍写的时候是将n个点和4m个询问的点都放在里一起进行排序然后用树状数组，但是由于离线 + 容斥了，就非常混乱，后来看一个很妙的思路就是分开排序，就是对n个点按x排，4m个点也按x排，用树状数组计算答案的时候，去遍历4m个点，用一个while循环先去尽可能插能插进去的点，再询问，就很妙，而且对于m次询问来说，将每次的询问拆成了如下的四部分：$ans(x2, y2)- ans(x2, y1 - 1)-ans(x1-1, y2)+(x1-1, y1-1)$,处理的方式如下：

for(int i = 1; i <= m; ++i){
     x1 = IntRead();y1 = IntRead();
     x2 = IntRead();y2 = IntRead();
     ++tot;ar[tot].id = tot;ar[tot].x = x2;ar[tot].y = y2;
     ++tot;ar[tot].id = tot;ar[tot].x = x2;ar[tot].y = y1  - 1;
     ++tot;ar[tot].id = tot;ar[tot].x = x1 - 1;ar[tot].y = y2;
     ++tot;ar[tot].id = tot;ar[tot].x = x1 - 1;ar[tot].y = y1 - 1;
}

将一个询问拆成四个，统计答案的时候就直接

for(int i = 1; i <= tot; i += 4){
     printf("%d\n", ans[i] + ans[i + 3] - ans[i + 1] - ans[i + 2]);
}

再有就是这个题的坐标的范围达到了1e7，巨大，需要离散化（不离散化吸口氧也行其实）,因为先通过排序降掉了第一维，所以我们只需要离散化第二维y即可，用vector排序去重二分来进行离散化操作，剩下的就是树状数组操作了，注意树状数组的update操作要跑到 n + 2 * m，因为离散化后最多有n + 2 * m个数

还有就是只需要对x排序，不需要对y进行排序，不然不吸氧是过不去的

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 1000000007
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
#define y1 y114514
#define MAX 2000000 + 50
int n, m, k, op;
int x1, x2, y1, y2;
struct ran{
    int x, y;
}tr[MAX];
bool cmp(ran a, ran b){
    if(a.x != b.x)return a.x < b.x;
    else return a.y < b.y;
}

int tot;
struct ranran{
    int x, y, id;
}ar[MAX];
bool cmpp(ranran a, ranran b){
    if(a.x != b.x)return a.x < b.x;
    else return a.y < b.y;
}

int sum[MAX];
inline int lowbit(int x){
    return x & (-x);
}
inline int getans(int i){
    int ans = 0;
    while (i) {
        ans += sum[i];
        i -= lowbit(i);
    }
    return ans;
}
inline void insert(int i, int c){
    while (i <= n + 2 * m) {
        sum[i] += c;
        i += lowbit(i);
    }
}
int ans[MAX];
void work(){
    n = IntRead();m = IntRead();
    vector<int>v;
    for(int i = 1; i <= n; ++i){
        tr[i].x = IntRead();tr[i].y = IntRead();
        v.push_back(tr[i].y);
    }
    for(int i = 1; i <= m; ++i){
        x1 = IntRead();y1 = IntRead();
        x2 = IntRead();y2 = IntRead();
        v.push_back(y2);v.push_back(y1 - 1);
        ++tot;ar[tot].id = tot;ar[tot].x = x2;ar[tot].y = y2;
        ++tot;ar[tot].id = tot;ar[tot].x = x2;ar[tot].y = y1  - 1;
        ++tot;ar[tot].id = tot;ar[tot].x = x1 - 1;ar[tot].y = y2;
        ++tot;ar[tot].id = tot;ar[tot].x = x1 - 1;ar[tot].y = y1 - 1;
    }
    sort(tr + 1, tr + 1 + n, cmp);
    sort(ar + 1, ar + 1 + tot, cmpp);
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(), v.end()), v.end());
    int cnt = 1;
    for(int i = 1; i <= tot; ++i){
        while (cnt <= n && tr[cnt].x <= ar[i].x) {
            int p = (int)(lower_bound(v.begin(), v.end(), tr[cnt].y) - v.begin());
            insert(p + 1, 1);
            ++cnt;
        }
        int p = (int)(lower_bound(v.begin(), v.end(), ar[i].y) - v.begin());
        ans[ar[i].id] += getans(p + 1);
    }
    for(int i = 1; i <= tot; i += 4){
        printf("%d\n", ans[i] + ans[i + 3] - ans[i + 1] - ans[i + 2]);
    }
}


int main(){
    work();
    return 0;
}