956. 最高的广告牌

题目描述：

你正在安装一个广告牌，并希望它高度最大。这块广告牌将有两个钢制支架，两边各一个。每个钢支架的高度必须相等。

你有一堆可以焊接在一起的钢筋 rods。举个例子，如果钢筋的长度为 1、2 和 3，则可以将它们焊接在一起形成长度为 6 的支架。

返回 广告牌的最大可能安装高度。如果没法安装广告牌，请返回 0 。

• 0 <= rods.length <= 20
• 1 <= rods[i] <= 1000
• sum(rods[i]) <= 5000

思路：

考虑动态规划

假设$dp[i][j][k]$表示前 i 个钢筋是否可以构成两个互不相交，和为j和k的集合

可以不选第 i 个钢筋 $dp[i][j][k]=dp[i-1][j][k]$

选第 i 个钢筋 $dp[i][j][k] |= dp[i-1][j-ar[i]][k]|dp[i-1][j][k-ar[i]]$

这样的复杂度是 $O(n*m*m)$，m为所有钢筋的长度和

一定会超时的

对于这种求两者长度关系的，我们可以考虑把二者的差作为状态，这样可以将j k 的二维状态降低成一维

所以我们考虑 $dp[i][j]$表示前 i 个钢筋，能选出两个互不相交的钢筋集合，长度和的差值为j的情况下，两个集合总长度的最大值

• 不选 i 时， $dp[i][j] = dp[i-1][j]$

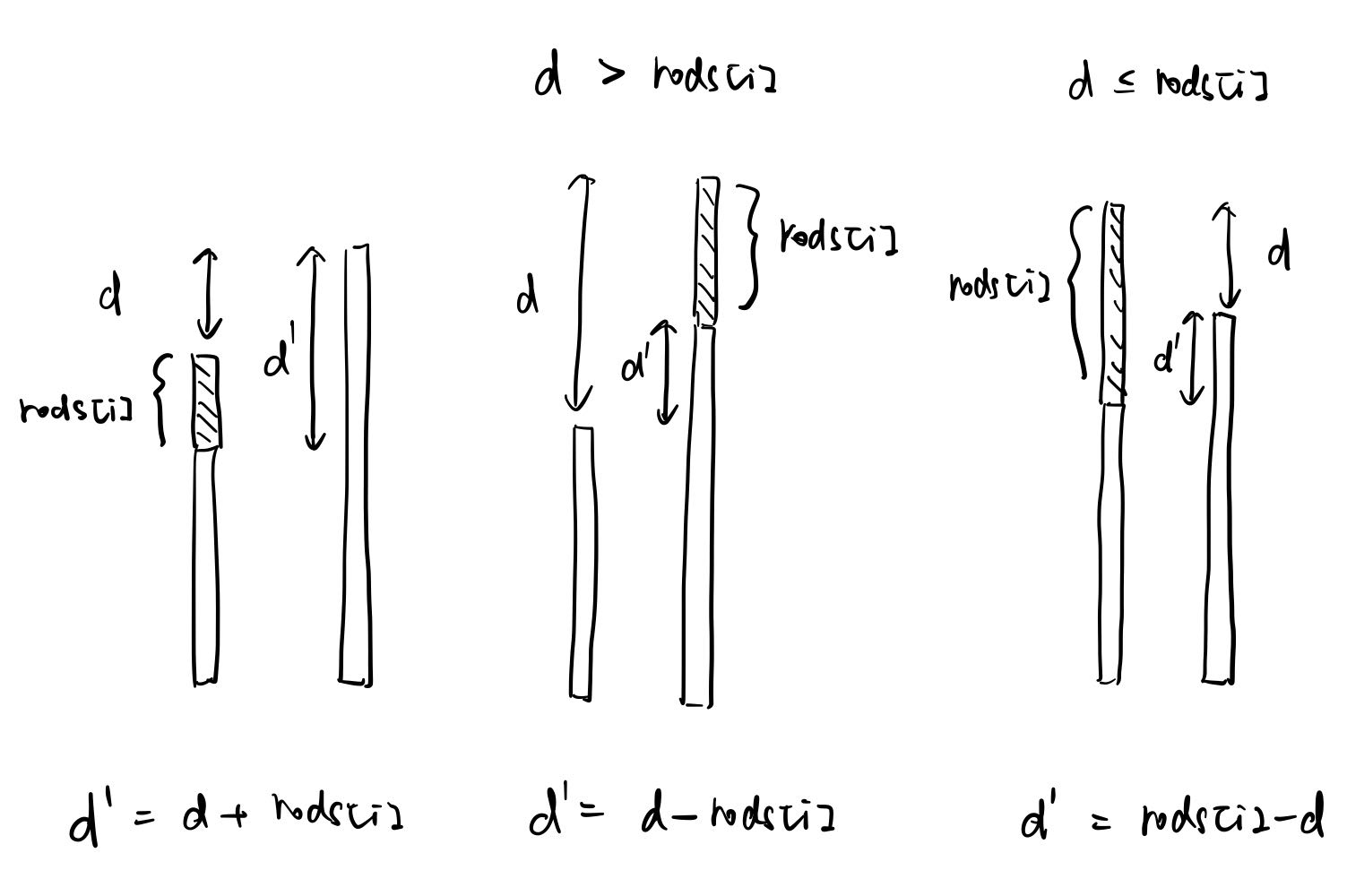
• 选 i 时，存在三种情况

  • 将第 i 根钢筋焊接在短的那一边后，长度高的依然是另一根：

    • $dp[i][j]=dp[i-1][j+ar[i]] + ar[i]$

  • 将第 i 根钢筋焊接在短的那一边后成为长度最高的那根：

    • $dp[i][j]=dp[i-1][ar[i]-j]$

  • 将第 i 根钢筋焊接在长的那一边后

    • $dp[i][j]=dp[i-1][j-ar[i]]$

class Solution {
public:
    int tallestBillboard(vector<int>& ar) {
        int n = ar.size(), m = 0;
        for(auto x : ar)m += x;
        vector<vector<int>>dp(n + 1, vector<int>(m + 1, -1));
        dp[0][0] = 0;
        for(int i = 1; i <= n; ++i){
            for(int j = 0; j <= m; ++j){
                dp[i][j] = dp[i - 1][j];
                if(j + ar[i - 1] <= m && dp[i-1][j + ar[i - 1]] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][j + ar[i - 1]] + ar[i - 1]);
                if(dp[i-1][abs(j - ar[i - 1])] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][abs(j - ar[i - 1])] + ar[i - 1]);
            }
        }
        return dp[n][0] / 2;
    }
};