L2-043 龙龙送外卖

题目描述：

给你n个点，m次询问，n个点构成一棵树

给出n个点，每个点的父节点

你现在在根结点，对于每次询问i，你都要回答，从根结点出发，至少经历1到i次询问的每个点1次，所需要的最短距离

思路：

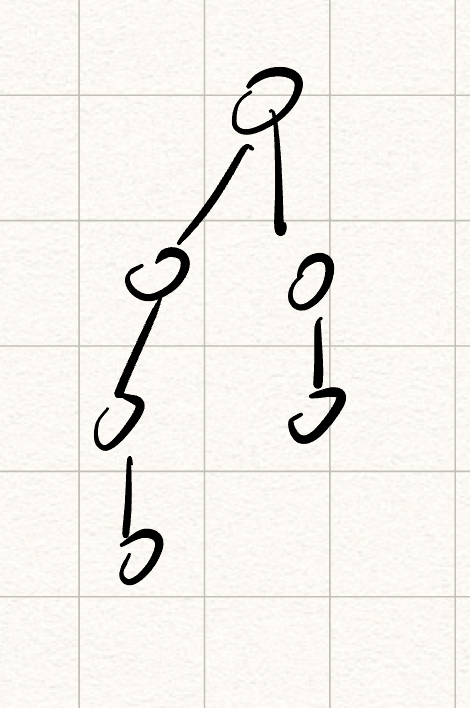
首先考虑给定一棵所有点的LCA都是根结点的树，从根结点出发经历所有的点后回到根结点的最短距离为：每个叶子结点的深度之和 * 2，具体图如下：

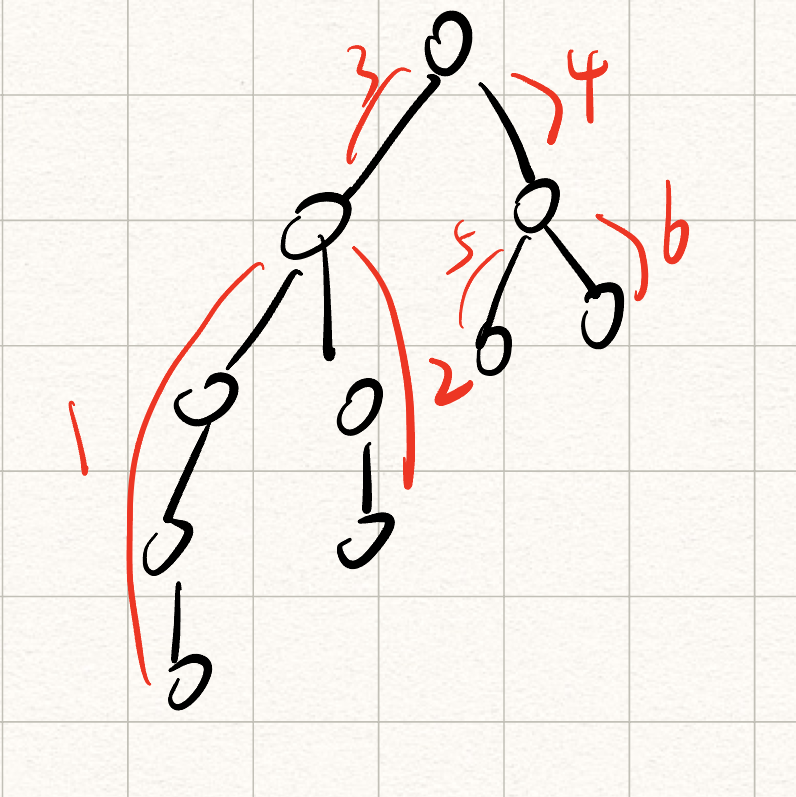
回到正常的树中，我们还是考虑从根结点出发经过所有点后回到根结点的情况，如下图：

则答案是：3+1+1+2+2+3+4+5+5+6+6+4，如果按照第一张图的方法，则3和4都会被多计算一次，可以发现3和4都是作为LCA的点

所以我们对于一颗树，我们可以从每个叶子结点开始往上遍历，每经过一个点，如果这个点没有被标记，则sum+=2，并将这个点给标记掉，表示上面的边不需要再多走一遍，如果被标记了就直接跳出，进入下一个叶子的遍历

而本题是不想要回到根结点的，所以我们可以用sum抛去一个深度最大的点，来使得最小值是最小的

所以对于每次询问，我们都从这个点开始往上遍历，如果这个点被访问过了，就return，否则就sum+2，标记这个点，然后往父节点进行遍历

再维护一个1到i的所有询问的点中深度的最大值mx，用sum – mx即可

#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define MAX 300050
int n, m, x;
int root;
vector<int>tr[MAX];
bool vis[MAX];
int fa[MAX];
int he[MAX];
void dfs(int u)
{
    he[u] = he[fa[u]] + 1;
    for(auto v : tr[u])
    {
        if(v == fa[u])continue;
        else
        {
            dfs(v);
        }
    }
}
int mx, sum;
void fuck(int x)
{
    if(vis[x])return;
    sum += 2;
    vis[x] = 1;
    fuck(fa[x]);
}

void work()
{
    cin >>n >>m;
    for(int i = 1; i <= n; ++i){
        cin >> x;
        fa[i] = x;
        if(x == -1){
            root = i;
        }
        else{
            tr[x].pb(i);
            tr[i].pb(x);
        }
    }
    fa[root] = 0;he[0] = -1;
    dfs(root);
    vis[root] = 1;
    while(m--){
        cin >> x;
        mx = max(mx, he[x]);
        fuck(x);
        cout << sum - mx  << endl;
    }
}

int main()
{
    work();
    return 0;
}