Codeforces Round #739 (Div. 3)
admin
|
|
330
|
Codeforces

2034 字
|
31 分钟

Codeforces Round #739 (Div. 3)

A. Dislike of Threes

题目描述：

如果一个数能被3整除或者十进制结尾的数字是3则是无趣的数，你想知道第n个有趣的数是什么

思路：

数据很小，直接暴力就可以

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t, n, m;
int tr[MAX];

inline bool judge(int x){
    if(x % 3 == 0)return false;
    if(x % 10 == 3)return false;
    return true;
}

int main(){
    sd(t);
    int tot = 0;
    for(int i = 1; i <= MAX; ++i){
        if(judge(i)){
            tr[++tot] = i;
            if(tot >= 1005)break;
        }
    }
    while (t--) {
        sd(n);
        cout<<tr[n]<<endl;
    }
    return 0;
}

B. Who's Opposite?

题目描述：

一个均匀的环，从1开始顺时针标到n，每个人都通过圆心看对面的人

你现在不知道圆圈的人数，但你知道a看着的人是b，你需要确定出c看着的人是谁，如果不存在这样的圆，则输出-1

思路：

不难发现，a和b肯定是在左右两边的，假设a小于，那b = a + n/2，假设k = b – a，如果c小于k，也就是c在前半圆，则c看着的人是c+k，否则是c-k，当然，如果n小于abc的任意一个则输出-1

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t, n, m;
int a, b, c;
int tr[MAX];


int main(){
    sd(t);
    while (t--) {
        sddd(a, b, c);
        if(a > b)swap(a, b);
        n = (b - a) * 2;
        if(n < c || n < a || n < b)cout<<-1<<endl;
        else{
            
            if(c > n / 2){
                int ans = (c + n / 2) % n;
                cout<<ans<<endl;
            }
            else{
                int ans = c + n / 2;
                cout<<ans<<endl;
            }
        }
    }
    return 0;
}

C. Infinity Table

题目描述：

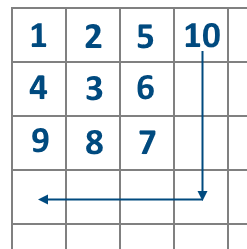
按照的方法填数字，问数字n的横纵坐标是多少

img

思路

不难发现，第一列是1 4 9 16……，刚好是平方数，所以我们可以预处理出来小于等于1e9的所有平方数，然后确定到n的位置，剩余的再模拟即可

当时差点脑子糊涂了用等差数列来算位置了，后来才发现直接是平方数

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t;
ll n, num;
ll tr[MAX];

int main(){
    
    for(int i = 1; ; ++i){
        tr[++num] = i * i;
        if(tr[i] >= 1000000000)break;
    }
    sd(t);
    while (t--) {
        scanf("%lld", &n);
        ll pos = lower_bound(tr + 1, tr + 1 + num, n) - tr;
        if(n == tr[pos]){
            cout<<pos<<' '<<1<<endl;
        }
        else{
            pos -= 1;
            ll x = pos + 1;
            n -= tr[pos];
            if(n > x){
                n -= x;
                cout<<x<<' '<<pos - n + 1<<endl;
            }
            else{
                cout<<n<<' '<<x<<endl;
            }
        }
    }
    return 0;
}

D. Make a Power of Two

题目描述：

对于一个十进制数，你有两种操作

  • 删掉任意一位数
  • 在最右边补任意一位数

你现在想知道任意一个数最少需要几次操作能变成2的幂次方

思路：

这个题比赛的时候确实是一眼就看出思路了，不过写起来挺麻烦，调了一个小时才调出来，还是太菜了(╥﹏╥)

思路大概是对每一个数n，拿他和0到63位2的幂次方都去跑一次匹配，这个匹配是2的幂次方必须连着取，但n可以不连续，这样的原因是操作2只能从数的最右边加数，不能在数中间加，如果可以在数中间加的话就相当于跑最大公共子序列的dp了。

n和每个数匹配的时候就更新一下最小值，最后输出就行

具体的放到代码里面讲，不过这个代码是比赛的时候写的，又臭又长，

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t, ans;
ll n, num, q;
ll tr[MAX];
vector<ll>v[100];


int main(){
    for(int i = 0; i <= 63; ++i){//预处理2的幂次方
        tr[i] = pow(2, i);
        ll p = tr[i];
        while (p) {
            v[i].push_back(p % 10);
            p /= 10;
        }
        reverse(v[i].begin(), v[i].end());
    }
    sd(t);
    while (t--) {
        vector<int>ar;//存数字n的所有数位
        scanf("%lld", &n);
        q = n;
        ans = (int)n;
        while (q) {
            ar.push_back(q % 10);
            q /= 10;
        }
        reverse(ar.begin(), ar.end());//颠倒一下
        for(int i = 0; i < 60; ++i){//和每个2的幂次都比较一下
            int pos = 0;//记录在n的位置
            int flag = 0;//记录匹配到2的幂次的哪个位置
            for(ll j = 0; j < v[i].size(); ++j){
                bool k = 0;
                while (pos < ar.size()) {
                    if(ar[pos] == v[i][j]){//匹配成功就标记一下
                        k = 1;
                        ++flag;
                        ++pos;
                        break;
                    }
                    ++pos;
                }
                if(k == 0)break;//如果没有被标记，说明此时2的幂次的第flag位数在n中不存在，那就跳出
            }
            ans = min(ans, (int)v[i].size() + (int)ar.size() - flag - flag);//跟新最小值
        }
        cout<<ans<<endl;
    }
    return 0;
}

E. Polycarp and String Transformation

题目描述：

有一个串s，每次都分别进行两种操作，先将串s接到t后面，然后删掉s中的一种字符（这里是全删，比如aaabbbc，删a，得到bbbc）直到s为空串。

现在给出操作后得到的串t，你需要推出s是什么，已经删除字符的顺序

思路：

切完D题，剩20分钟，我看了这个题，没有思路，就看F1去了，但是这个题其实也挺简单，可能是当时调D调自闭了，没仔细思路

仔细想想就能发现，从串t的最后一个开始，依次出现的不同的字符就是删除的顺序的倒序

假设原来的串s中每个字母出现的次数为num[i],则给的这个t根据删除顺序，t中每个字符出现的次数应该是 i * num[j]，i是值第i个被删除，num[j]指的是第i个被删除的字符出现的次数，所以我们统计一下t串中每个字符出现的次数，看看能不能除尽这个字符的删除位置，但凡有一个不难，则输出-1

那如何得到串s？其实第一次操作的时候就将s贴到t上了，所以如果有答案，则一定是t串的前位

我们取出来，设为str，看看str的每个字符的数量是不是和num相同，如果不同就输出-1，再用这个str根据题目要求去模拟，看看最后能不能造出t，如果可以就输出，不可以就输出-1

思路主要是模拟+特判，写起来也不是那么简洁

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  1000000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int p, k;
string s, t, ss, tt;
int num[30];
int cnt[30];
bool vis[30];

void work(){
    s = ss = "";
    mem(num, 0);
    mem(cnt, 0);
    mem(vis, 0);
    cin>>t;
    vector<int>v;
    for(int i = (int)t.size() - 1; i >= 0; --i){
        if(num[t[i] - 'a' + 1] == 0){
            s += t[i];
            v.push_back(t[i] - 'a' + 1);
        }
        ++num[t[i] - 'a' + 1];
    }
    reverse(s.begin(), s.end());
    reverse(v.begin(), v.end());
    int sum = 0;
    for(int i = 0; i < v.size(); ++i){
        if(num[v[i]] % (i + 1) != 0){
            cout<<-1<<endl;
            return;
        }
        num[v[i]] /= (i + 1);
        sum += num[v[i]];
    }
    for(int i = 0; i < sum; ++i){
        ++cnt[t[i] - 'a' + 1];
    }
    for(int i = 1; i <= 26; ++i){
        if(num[i] != cnt[i]){
            cout<<-1<<endl;
            return;
        }
    }
    for(int i = 0; i < sum; ++i)ss += t[i];
    tt = ss;
    for(int i = 0; i < v.size(); ++i){
        vis[v[i]] = 1;
        for(int j = 0; j < ss.size(); ++j){
            if(!vis[ss[j] - 'a' + 1])tt += ss[j];
        }
    }
    if(tt != t){
        cout<<-1<<endl;
        return;
    }
    else{
        cout<<ss<<' '<<s<<endl;
    }
}

int main(){
    sd(p);
    while (p--) {
        work();
    }
    return 0;
}

F. Nearest Beautiful Number

题目描述：

F1和F2差不多，就是k的取值范围变了

给你一个数n和k，你可以使用小于等于k种数字，造一个大于等于n的最小的数

思路：

切完D剩的20分钟就在搞F1，一直分类讨论，没讨论出来，睡觉的时候就在想第二天起来一定要写dfs，结果起来又在分类讨论，写了一百五十多行，一直wa2，受不了了，就换了个思路开始枚举暴力

用字符串来处理，下面我把n都叫做s

首先对于k=1，特判调，要么是全是s[0]，要么全是s[0] + 1

其他的，就从最低位开始模拟，假设当前模拟到第i位，对第i位，从s[i]枚举到9，每次都判断一下，前i个中有几个不同的字符，计为cnt，如果小于k，则可以更新答案，0到i位就不用动了，如果cnt=k，则后面几位放前i位的最小值，如果cnt < k，则后面几位放0. 然后每次都更新最小值即可

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1.0E-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  1000000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
//#define min(a,b) (((a)>(b)) ? (b):(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t, k;
string s;

int getnum(string s){
    set<char>se;
    for(int i = 0; i < s.size(); ++i)se.insert(s[i]);
    return (int)se.size();
}

int string_to_int(string s){
    int sum = 0;
    for(int i = 0; i < s.size(); ++i){
        sum *= 10;
        sum += s[i] - '0';
    }
    return sum;
}

void work(){
    cin>>s>>k;
    
    if(getnum(s) <= k){
        cout<<s<<endl;
        return;
    }
    if(k == 1){
        int a = s[0] - '0';
        int ans = 0;
        for(int i = 0; i < s.size(); ++i){
            ans *= 10;
            ans += a;
        }
        if(ans >= string_to_int(s))cout<<ans<<endl;
        else{
            for(int i = 0; i < s.size(); ++i)cout<<(char)(s[0] + 1);
            cout<<endl;
            return;
        }
    }
    else{
        int ans = inf;
        int cnt = 0;
        while (s.size()) {
            while (s[s.size() - 1] < '9') {
                s[s.size() - 1]++;
                string cur = s;
                int num = getnum(s);
                if(num <= k){
                    char minx = '9';
                    for(int i = 0; i < s.size(); ++i)minx = min(minx, s[i]);
                    for(int i = 1; i <= cnt; ++i)cur += (num == k) ? minx : '0';
//                    cout<<cur<<endl;
                    ans = min(ans, string_to_int(cur));
                }
            }
            s.pop_back();
            ++cnt;
        }
        cout<<ans<<endl;
    }
}


int main(){
    sd(t);
    while (t--) {
        work();
    }
    return 0;
}

 

博客内容均系原创，未经允许严禁转载！
cf
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
Educational Codeforces Round 112 (Rated for Div. 2) 「D. Say No to Palindromes」

							
							

							
Educational Codeforces Round 117 (Rated for Div. 2) D. X-Magic Pair 「思维 + 辗转相除优化」

							
							

							
Educational Codeforces Round 115 (Rated for Div. 2) D. Training Session

							
							

							
Codeforces Round #744 (Div. 3)

							
							

							
Lemonade Trade「dp + 对数优化」