贪心算法知识总结
admin
|
|
390
|
算法知识总结

2163 字
|
27 分钟

区间贪心

最小点覆盖问题

题目描述：

给n个区间，再数轴上选尽量少的点，使得每个区间至少包含一个选出的点

思路：

按区间右端点从小到大排列

取一个当前点p，然后从头开始遍历，如果当前区间被当前的这个p点覆盖了，那就continue，如果没覆盖成功，那就更新答案，并将当前区间的右端点作为当前的点

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
ll a, b, c;
string s, t;

struct ran{
    int l, r;
}tr[MAX];

bool cmp(ran a, ran b){
    return a.r < b.r;
}

void work(){
    cin >> n;
    for(int i = 1; i <= n; ++i){
        cin >> tr[i].l >> tr[i].r;
    }
    sort(tr + 1, tr + 1 + n, cmp);
    int ans = 1;
    int p = tr[1].r;
    for(int i = 2; i <= n; ++i){
        if(tr[i].l <= p && tr[i].r >= p)continue;
        else{
            ++ans;
            p = tr[i].r;
        }
    }
    cout << ans << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

最大不交区间数量问题

题目描述：

给n个区间，选尽可能多的数量的区间，满足这些区间互不相交

思路：

和最小点覆盖问题的解法一模一样

代码也同上

求不交区间组问题

题目描述：

n个区间，分成尽可能少的组，使得每个组的区间互不相交

思路：

按区间的左端点从小到大排序，再用一个优先队列(小根堆)存每个组的区间的最大r，这样来一个新的区间的时候，可以直接取队首进行判断，如果当前区间的左端点比队首还小，就需要重开一个组放这个区间，也就是将该区间的右端点塞到优先队列里面；如果当前区间的左端点比优先队列的队首大，那就弹出队首，把该区间的右端点塞进去

最后输出优先队列大小即可

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
ll a, b, c;
string s, t;

struct ran{
    int l, r;
}tr[MAX];

bool cmp(ran a, ran b){
    return a.l < b.l;
}

void work(){
    cin >> n;
    for(int i = 1; i <= n; ++i){
        cin >> tr[i].l >> tr[i].r;
    }
    sort(tr + 1, tr + 1 + n, cmp);
    priority_queue<int, vector<int>, greater<int>>q;
    q.push(tr[1].r);
    for(int i = 2; i <= n; ++i){
        if(tr[i].l > q.top()){
            q.pop();
            q.push(tr[i].r);
        }
        else{
            q.push(tr[i].r);
        }
    }
    cout << q.size() << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

最少区间覆盖线段问题

题目描述：

给n个区间和一个线段区间，问最少需要几个区间能覆盖掉这个线段区间，如果不能完全覆盖，则输出-1

思路：

排序 + 双指针

设[l, r]为待覆盖的区间，将n个区间按左端点从小到大排序，从头开始枚举区间，通过双指针来取得左端点小于等于 l 的中的最大的 r，作为新的 l，再接着找下去，满足题意就输出答案，不满足就输出-1

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
struct ran{
    int l, r;
}tr[MAX];

bool cmp(ran a, ran b){
    if(a.l != b.l)return a.l < b.l;
    else return a.r > b.r;
}

void work(){
    int l, r;
    cin >> l >> r;
    cin >> n;
    rep(i, 1, n)cin >> tr[i].l >> tr[i].r;
    sort(tr + 1, tr + 1 + n, cmp);
    int ans = 0;
    for(int i = 1; i <= n; ++i){
        int j = i, ed = -inf;
        while (j <= n && tr[j].l <= l) {//双指针找右端点
            ed = max(ed, tr[j].r);
            ++j;
        }
        if(ed < l){//判断是否无法完全覆盖
            cout << -1 << endl;
            return;
        }
        ++ans;//更新答案
        if(ed >= r){//如果已经成功覆盖就输出
            cout << ans << endl;
            return;
        }
        l = ed;//更新l
        i = j - 1;//j位置不满足上次的l，但可能满足更新后的l，所以i要跳到j-1处，结束循环后会执行++i的操作，i就变成了j，就可以重新判断j了
    }
    cout << -1 << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

Huffman树贪心

合并果子

题目描述：

n个果子，每个果子都有一个重量，每一次合并，可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。问合并成一堆时消耗的最少体力是多少

思路：

经典的优先队列问题

很显然这个过程形成了一个二叉树，n个果子就是二叉树的n个叶子，我们假设叶子结点的深度是h[i]，那这个果子产生重量的贡献其实就是重量w[i] * h[i]，要使得消耗的体力最小，则需要满足哈夫曼树的方式，优先取两堆重量最小的进行合并…

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
ll a, b, c;
string s, t;
int tr[MAX];

void work(){
    cin >> n;
    priority_queue<int>q;
    while (n--) {
        cin >> x;
        q.push(-x);
    }
    ll ans = 0;
    while (q.size() != 1) {
        y = q.top();q.pop();
        y += q.top();q.pop();
        ans -= y;
        q.push(y);
    }
    cout << ans << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

排序不等式

排队打水

题目描述：

有 n个人排队到 1 个水龙头处打水，第 i 个人装满水桶所需的时间是 ti，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

思路：

简单的贪心，从小到大排序即可

这里我们用一个通俗的方式进行推导：

假设最终排序后的结果是a排在b前面，则说明a排在b前面时，a和b对等待时间产生的贡献应该小于等于b排在a前面，同时有一点值得说明的是：a和b不会影响排在其前面的人打水时间，也不会影响后面的人打水的时间，所以我们只需要计算a和b的即可简单代替总时间

  • a排在b前时，设a开始打水是第 时刻，则a等待的时间就是 ,b等待的时间就是
  • b排在a前时，同样的b等待的时间是 ，而a等待的时间是

我们刚刚规定a排在b前面，则说明 ，简单化简一下也就是

也就是说a排在b前面的充要条件是

<img src="/Users/chelsea/Library/Application Support/typora-user-images/image-20220120230651388.png" alt="image-20220120230651388" style="zoom:50%;" /

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
ll a, b, c;
string s, t;
int tr[MAX];

void work(){
    cin >> n;
    rep(i, 1, n)cin >> tr[i];
    sort(tr + 1, tr + 1 + n);
    ll ans = 0;
    ll t = 0;
    for(int i = 1; i <= n; ++i){
        ans += t;
        t += tr[i];
    }
    cout << ans << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

绝对值不等式

货仓选址

题目描述：

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

思路：

这是一个绝对值不等式的问题

假设货仓的位置为x，则货仓到每家商店的距离之和为 , 我们可以将其中 i 个和第 n - i + 1个进行结合

每个组就是 ，意义是x到两个点的距离，显然要想使得这个距离最短，就得将x放在二者中间，此时距离和最短，为

所以我们只需要将n个位置从小到大排个序，分成 n / 2个组分别计算就行，而且我们可以知道 x 就是这n个数的中位数，如果n是偶数，也没关系，他可以是中间那个两个数之间的任意一个数，反正距离和是不变的

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
ll a, b, c;
string s, t;
int tr[MAX];

void work(){
    cin >> n;
    rep(i, 1, n)cin >> tr[i];
    sort(tr + 1, tr + 1 + n);
    ll sum = 0;
    for(int i = 1; i <= n / 2; ++i){
        sum += tr[n - i + 1] - tr[i];
    }
    cout << sum << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

推公式类不等式贪心

耍杂技的牛

题目描述：

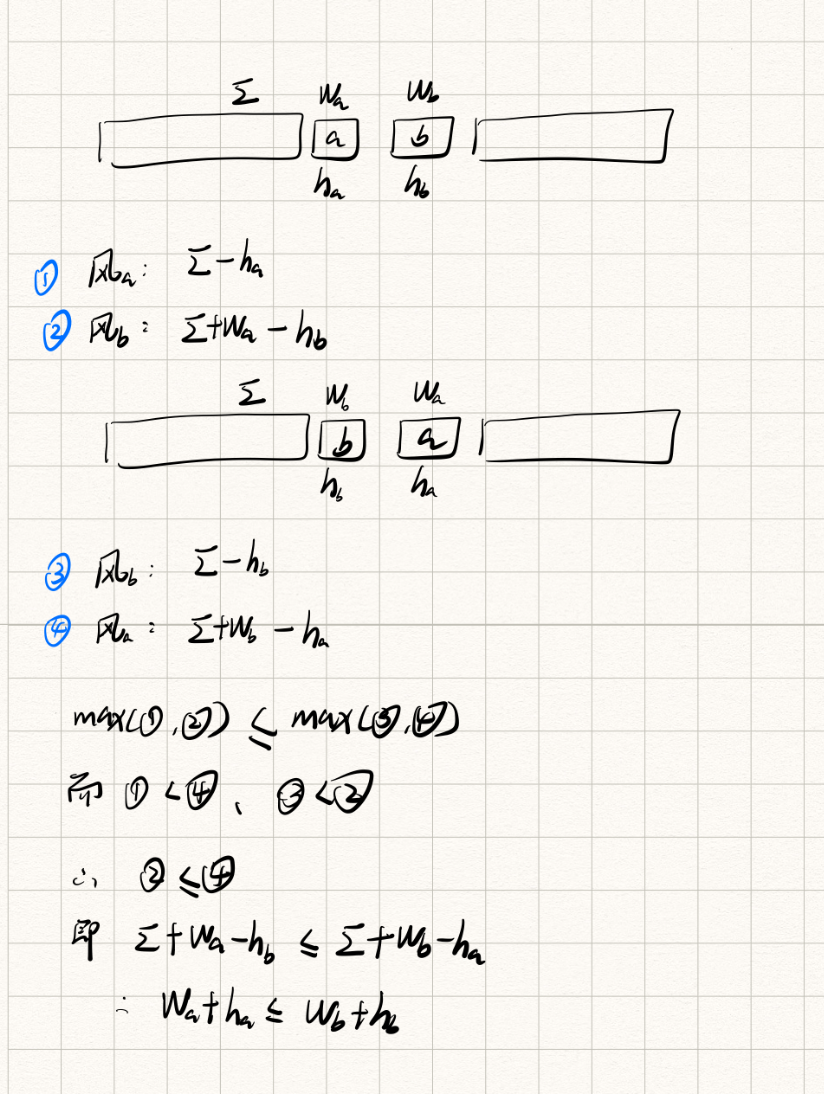
n个奶牛叠罗汉，从低到高一个接一个叠起来，每个奶牛都有一个重量w[i],和他的强壮度h[i],一个奶牛的风险值是在他上面所有奶牛的重量和-他自身的强壮度h[i]，我们的任务是确定奶牛的排序，使得所有奶牛的风险值中的最大值尽可能的小，并求出这个值

思路：

这个题和上面的排序不等式差不多，但是又涉及到最值问题，又有点不同，分成四个部分， ,但观察可见 ，那要使得 成立，则是前一个取2，后一个取4，因为1已经失败了，3也已经失败了，所以我们只需要使得2 <= 4即可，也就是推出 ，将其作为排序的方法即可

image-20230309110851606

//Work by: Chelsea
#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 998244353
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, op;
struct ran{
    ll s, w;
}tr[MAX];

bool cmp(ran a, ran b){
    return a.s + a.w < b.s + b.w;
}

void work(){
    cin >> n;
    rep(i, 1, n)cin >> tr[i].w >> tr[i].s;
    sort(tr + 1, tr + 1 + n, cmp);
    ll ans = -inf;
    ll sum = 0;
    for(int i = 1; i <= n; ++i){
        ans = max(ans, sum - tr[i].s);
        sum += tr[i].w;
    }
    cout << ans << endl;
}


int main(){
    io;
    //int tt;cin>>tt;
    //for(int _t = 1; _t <= tt; ++_t){
    //printf("Case #%d: ", _t);
    work();
    //}
    return 0;
}

 

博客内容均系原创，未经允许严禁转载！
贪心
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇