蓝桥杯2019 年B组C++国赛
admin
|
|
383
|
杂项

2761 字
|
35 分钟

平方序列

题目描述：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xgsSbJ4I-1622462563124)(/Users/chelsea/Library/Application Support/typora-user-images/image-20210531161138113.png)]

思路：

直接枚举x和y即可

优化一点的方法是：只枚举x，根据2x2 = 20192 + y2,来判断y是否是整数即可

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

int main(){
    for(int x = 2020; x <= 10000; ++x){
        int a = 2 * x * x - 2019 * 2019;
        int y = sqrt(a);
        if(a == y * y){
            cout<<x + y<<endl;
            break;
        }
    }
    return 0;
}

质数拆分

题目描述：

将 2019拆分为若干个两两不同的质数之和，一共有多少种不同的方法？

注意交换顺序视为同一种方法，例如 2+2017=2019 与 2017 + 2 = 2019 视为同一种方法。

思路：

这个题有个很坑的点是“若干个”，这样的话就不能用dfs了，根本跑不出来，只能用动态规划了

有点类似于01背包，对于每个质数都有两种状态，选或者不选

dp[i] [j] 表示前i个物品，凑出j的方法数

dp[i] [j] = dp[i – 1] [j] + dp[i – 1] [j – tr[i]]

二维初始化的比较麻烦：dp[0] [0] = 1; dp[0] [j] = 0, 1<=j<=2019

还可以利用01背包的滚动数组来优化

dp[i] += dp[i – tr[j]]

初始化：dp[0] = 0;

还有个巨坑巨坑的点就是，得开longlong！！！

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

bool judge(int x){
    if(x == 1)return false;
    for(int i = 2; i * i <= x; ++i){
        if(x % i == 0)return false;
    }
    return true;
}

ll dp[2020][2020];
int tr[MAX];
int tot;

int main(){
    for(int i = 1; i <= 2019; ++i){
        if(judge(i))tr[++tot] = i;
    }
    dp[0][0] = 1;
    for(int i = 1; i <= 2019; ++i)dp[0][i] = 0;
    for(int i = 1; i <= tot; ++i){
        for(int j = 0; j <= 2019; ++j){
            if(j >= tr[i])dp[i][j] = dp[i - 1][j] + dp[i - 1][j - tr[i]];
            else dp[i][j] = dp[i - 1][j];
        }
    }
    cout<<dp[tot][2019]<<endl;
    return 0;
}


#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

bool judge(int x){
    if(x == 1)return false;
    for(int i = 2; i * i <= x; ++i){
        if(x % i == 0)return false;
    }
    return true;
}

ll dp[2020];
int tr[MAX];
int tot;

int main(){
    for(int i = 1; i <= 2019; ++i){
        if(judge(i))tr[++tot] = i;
    }
    dp[0] = 1;
    for(int i = 1; i <= tot; ++i){
        for(int j = 2019; j >= tr[i]; --j){
            dp[j] += dp[j - tr[i]];
        }
    }
    cout<<dp[2019]<<endl;
    return 0;
}

拼接

题目描述

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tJCJ53sw-1622462563125)(/Users/chelsea/Library/Application Support/typora-user-images/image-20210531181506067.png)]

思路：

这个题坑点很多很多，不好想明白，就算想明白了也会写wa

所以，最主要的是看懂题，想清楚这是个什么问题，该如何下手

这个题其实是问你，n * n个小正方形，能有多少种切割方式（大致方向是左上到右下），使得小正方形不被破坏，且分割后左右两个部分都关于y=x对称

由于是关于y=x对称的，那么我们就找一半即可

所以正解：让对角线上的每个点往右面去dfs（因为对称），四个方向去跑，当x到达7的位置，就++ans，

坑点：

  • 当你的y=0时，是不可以往上面走的，因为如果往上走，就将整个图形分成了三部分，这是不允许的
  • 不能越过对角线，也不能碰对角线，因为起点在对角线上，如果再次遇到了对角线，就相当于在图形里面挖了一个小正方形，这是不允许的
  • 不能出界
  • 线不能有交叉
#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

int n, ans;
bool vis[10][10];
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};

bool judge(int x, int y){
    if(vis[x][y])return false;
    if(x < 0 || x > n || y < 0 || y > n)return false;
    return true;
}

void dfs(int x, int y){
    if(x == n){
        ++ans;
        return;
    }
    for(int i = 0; i < 4; ++i){
        int xx = x + dx[i];
        int yy = y + dy[i];
        if((y == 0 && i == 1) || (!judge(xx, yy)) || yy >= xx)continue;
        vis[xx][yy] = 1;
        dfs(xx, yy);
        vis[xx][yy] = 0;
    }
    return;
}

int main(){
    n = 7;
    for(int i = 0; i <= n; ++i)dfs(i, i);
    cout<<ans<<endl;
    return 0;
}

求值

题目描述：

学习了约数后，小明对于约数很好奇，他发现，给定一个正整数 tt，总是可以找到含有 tt 个约数的整数。小明对于含有 tt 个约数的最小数非常感兴趣，并把它定义为 S_tS**t 。

例如 S1 = 1, S2 = 2, S3 = 4, S4 = 6，· · ·

现在小明想知道，当 t = 100 时，St 是多少？即 S100 是多少？

思路：

暴力枚举

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

int getnum(int x){
    int num = 0;
    for(int i = 1; i <= x; ++i){
        if(x % i == 0)++num;
    }
    return num;
}

int main(){
    for(int i = 1; i <= 100000; ++i){
        if(getnum(i) == 100){
            cout<<i<<endl;
            break;
        }
    }
    return 0;
}

路径计数

题目描述：

从一个 5×5 的方格矩阵的左上角出发，沿着方格的边走，满足以下条件的路线有多少种？

  1. 总长度不超过 12；
  2. 最后回到左上角；
  3. 路线不自交；
  4. 不走出 5×5 的方格矩阵范围之外。 如下图所示，ABC 是三种合法的路线。注意 B 和 C 由于方向不同，所以 视为不同的路线。

图片描述

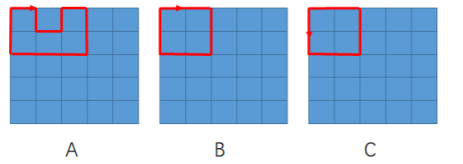
思路：

直接dfs就完事

这个题的官方答案出错了，应该是206，不是202，202是4 * 4的矩阵，而本题是5 * 5的矩阵

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

int ans;
int dx[] = {1, 0, -1, 0};
int dy[] = {0 ,1, 0, -1};
bool vis[10][10];
bool judge(int x, int y){
    if(vis[x][y])return false;
    if(x > 5 || x < 0 || y > 5 || y < 0)return false;
    return true;
}

void dfs(int x, int y, int num){
    if(num > 12)return;
    if(x == 0 && y == 0 && num > 2){
        ++ans;
        return;
    }
    for(int i = 0; i < 4; ++i){
        int xx = x + dx[i];
        int yy = y + dy[i];
        if(judge(xx, yy)){
            vis[xx][yy] = 1;
            dfs(xx, yy, num + 1);
            vis[xx][yy] = 0;
        }
    }
    return;
}

int main(){
    dfs(0, 0, 0);
    cout<<ans<<endl;
    return 0;
}

最优包含

题目描述：

我们称一个字符串 S 包含字符串 T 是指 T 是 S 的一个子序列，即可以从字符串 S 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 T 完全一样。

给定两个字符串 S 和 T，请问最少修改 S 中的多少个字符，能使 S 包含 T ？

其中，1 <= |T| <= |S| <= 1000

思路：

动态规划

dp[i] [j] 表示s的前i个包含t的前j个字符所需要修改的最少字符是多少

当s[i] = t[j]时，也就是字符相同时，就代表这个字符不需要进行修改，故dp[i] [j] = dp[i – 1] [j – 1]

当s[i] != t[j]时，也就是有可能得修改，修改的话就是dp[i – 1] [j – 1] + 1, 还有可能是之前就已经包含住他了， 就是dp[i – 1] [j]，所以dp[i] [j] = min(dp[i – 1] [j – 1] + 1, dp[i – 1] [j])

初始化：

开始都初始化为∞，然后让dp[i] [0] = 0,也就是没有j = 0的时候就不需要修改

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！

int dp[1005][1005];
string s, t;

int main(){
    cin>>s>>t;
    s = " " + s;
    t = " " + t;
    mem(dp, inf);
    dp[0][0] = 0;
//    for(int i = 1; i <= t.size(); ++i)dp[0][i] = 0;
    for(int i = 1; i <= s.size(); ++i)dp[i][0] = 0;
    for(int i = 1; i <= s.size(); ++i){
        for(int j = 1; j <= t.size(); ++j){
            if(s[i] == t[j]){
                dp[i][j] = dp[i - 1][j - 1];
            }
            else dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j]);
        }
    }
    cout<<dp[s.size()][t.size()]<<endl;
    return 0;
}

排列数

题目描述：

在一个排列中，一个折点是指排列中的一个元素，它同时小于两边的元素，或者同时大于两边的元素。

对于一个 1 ∼ n 的排列，如果可以将这个排列中包含 t 个折点，则它称为一个 t + 1 单调序列。

例如，排列 (1,4,2,3) 是一个 3 单调序列，其中 4 和 2 都是折点。

给定 n 和 k, 请问 1 ∼ n 的所有排列中有多少个 k单调队列？

思路：

我们根据给出的条件可以看出是全排序问题，且数据量可能很大，暴力有可能过不了，考虑使用动态规划来递推状态，解题思路如下：

  • 定义状态方程

    • 定义 dp[i][j] 为排列到第i位时有j个折点的方案数。dp[1] [0]=1 ,dp[k] [0]=2,k>1即顺序排列和倒序排列，都没有折点。

  • 定义转移方程

    • 对于当前 i 个数的排列，插入i+1 将得到新的排列，有 i+1 个插入位置可选，不同的位置插入对折点数的变化影响不同。

图片描述

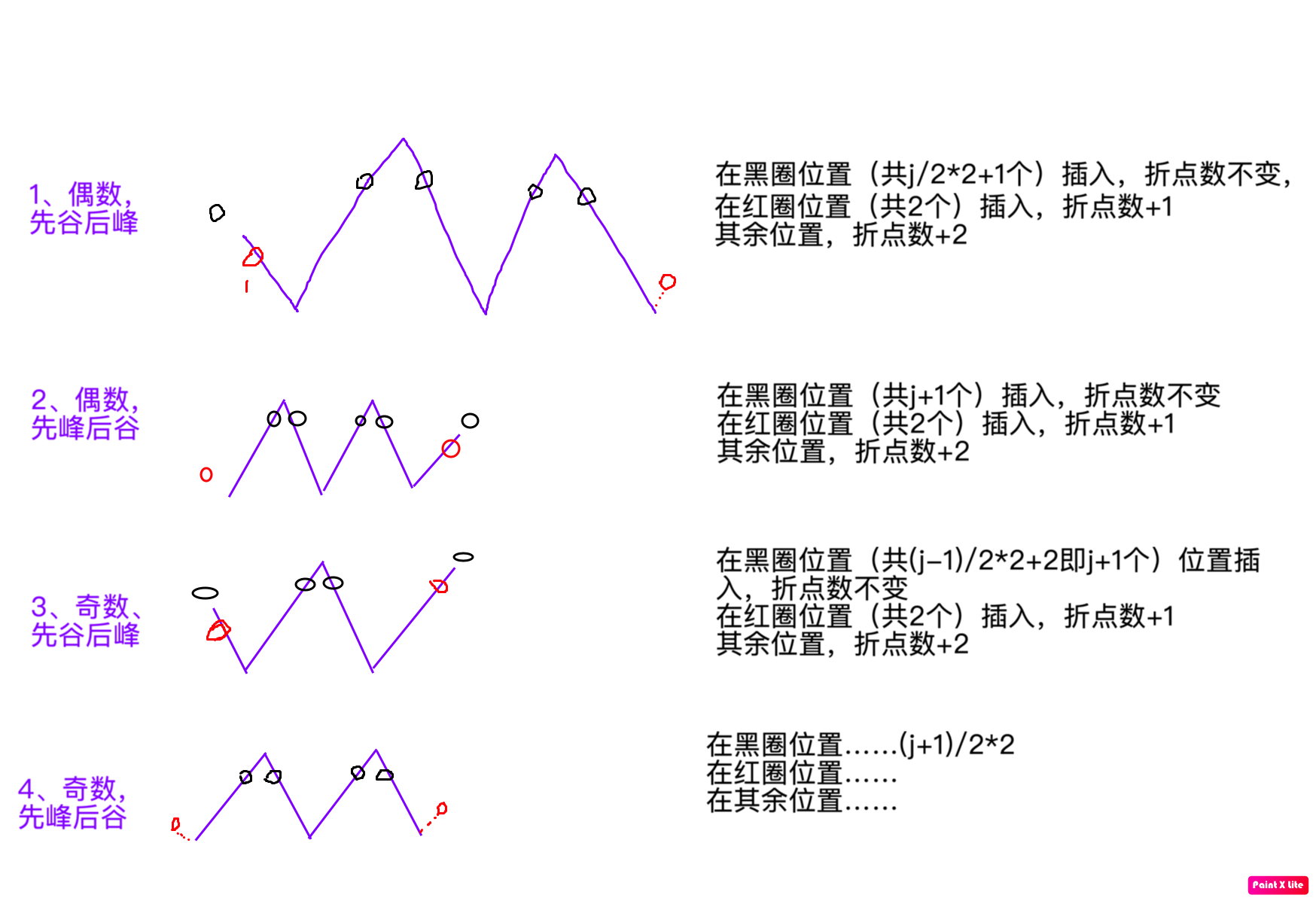
总结起来就是:

dp[i+1][j] += dp[i][j] *(j+1);
dp[i+1][j+1] += dp[i][j]*2;
dp[i+1][j+2] += (dp[i][j]*(i-j-2));

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 123456
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗！
//inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-'){f = -1;}ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;}
//inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9){print(x / 10);}putchar(x % 10 + '0');}
inline ll llRead(){ll x(0), t(1);char o (getchar());while (o < '0' || o > '9') {if (o == '-') {t = -1;}o = getchar();}for (; o >= '0' && o <= '9'; o = getchar()) {x = (x << 1) + (x << 3) + (o ^ 48);}return x * t;}
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}
ll qpow(ll a,ll n){ll ans=1,base=a%mod;while(n){if(n&1)ans=(ans*base)%mod;base=(base*base)%mod;n>>=1;}return ans;}
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }

ll dp[1005][1005];
int n, k;

int main(){
    cin>>n>>k;
    dp[1][0] = 1;
    for(ll i = 2; i <= n; ++i){
        dp[i][0] = 2;
        for(ll j = 0; j <= i - 2; ++j){
            dp[i + 1][j] = (dp[i + 1][j] + (dp[i][j] * (j + 1)) % mod) % mod;
            dp[i + 1][j + 1] = (dp[i + 1][j + 1] + (dp[i][j] * 2 ) % mod) % mod;
            dp[i + 1][j + 2] = (dp[i + 1][j + 2] + (dp[i][j] * (i - j - 2) % mod)) % mod;
        }
    }
    cout<<dp[n][k - 1] % mod<<endl;
    return 0;
}

解谜游戏

img

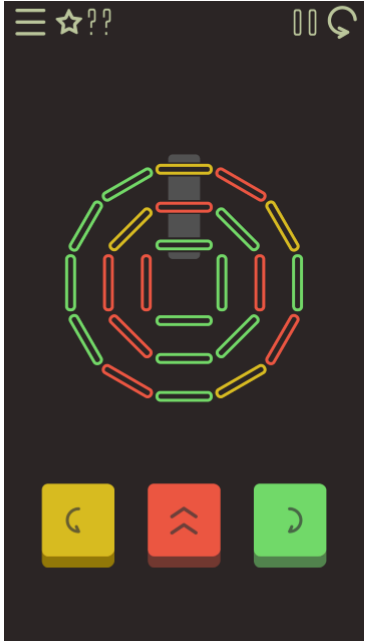
小明正在玩一款解谜游戏。谜题由 24 根塑料棒组成，其中黄色塑料棒 4 根，红色 8 根，绿色 12 根 (后面用 Y 表示黄色、R 表示红色、G 表示绿色)。初始时这些塑料棒排成三圈，如上图所示，外圈 12 根，中圈 8 根，内圈 4 根。

小明可以进行三种操作：

  1. 将三圈塑料棒都顺时针旋转一个单位。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么顺时针旋转一次之后，外圈、中圈、内圈依次变为：GYRYGRYGRGGG、 YRGRGGRR 和 RGGG。
  2. 将三圈塑料棒都逆时针旋转一个单位。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么逆时针旋转一次之后，外圈、中圈、内圈依次变为：RYGRYGRGGGGY、 GRGGRRYR 和 GGRG。
  3. 将三圈 0 点位置的塑料棒做一个轮换。具体来说：外圈 0 点塑料棒移动到内圈 0 点，内圈 0 点移动到中圈 0 点，中圈 0 点移动到外圈 0 点。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么轮换一次之后，外圈、中圈、内圈依次变为：RRYGRYGRGGGG、GGRGGRRY 和 YGGR。

小明的目标是把所有绿色移动到外圈、所有红色移动中圈、所有黄色移动到内圈。给定初始状态，请你判断小明是否可以达成目标？

思路：

因为三个是一起转的，棍少的就转的多，有些棍子就固定了能和谁交换，其他的换不成，就像4棍的第一个只能和8棍的第一个第五个，12棍的第一个第五个第9个，其他的同理

所以我们只需要统计每组是不是都是YRRGGG即可

#include<map>
#include<set>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<limits.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define seed 13331
#define mod 1000000007
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
typedef unsigned long long ull;


string a, b, c, s;
int x, y, z;

int main(){
    int n;
    cin>>n;
    while (n--) {
        cin>>c>>b>>a;
        bool k = 0;
        for(int i = 0; i < 4; ++i){
            x = 0;y = 0;z = 0;
            s = "";
            s += a[i];
            s += b[i];s += b[i + 4];
            s += c[i];s += c[i + 4];s += c[i + 8];
//            cout<<s<<endl;
            for(int j = 0; j < s.size(); ++j){
                if(s[j] == 'Y')++x;
                if(s[j] == 'R')++y;
                if(s[j] == 'G')++z;
            }
            if(!(x == 1 && y == 2 && z == 3)){
                k = 1;
            }
        }
        if(!k)cout<<"YES\n";
        else cout<<"NO\n";
    }
    
    return 0;
}

第八大奇迹

猫了一眼题面，一看就知道是主席树，等我学了再回来做

燃烧权杖

概率dp？（第十题，一般做不出来，先放放

 

博客内容均系原创，未经允许严禁转载！
蓝桥杯
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
蓝桥杯2016年B组C++国赛题解

							
							

							
蓝桥杯2018年C++组国赛

							
							

							
蓝桥杯2017年B组C++国赛

							
							

							
第十二届蓝桥杯省赛第一场C++A组 「左孩子右兄弟」

							
							

							
第十一届蓝桥杯省赛第一场C++A/B组真题题解