电力

题目描述：

给定一个由 n 个点 m 条边构成的无向图，请你求出该图删除一个点之后，连通块最多有多少。

思路：

对于一个连通图，肯定是删除图内割点才能产生更多的连通分量

所以我们可以枚举删除每个割点，找到删除该割点后能产生的最大的连通分量数量maxn,再统计整个图的连通块的数量num,则答案就是maxn + num - 1

怎么求删除一个割点能产生的连通分量的数量？

我们只需要计算该割点能形成多少个点双连通分量即可

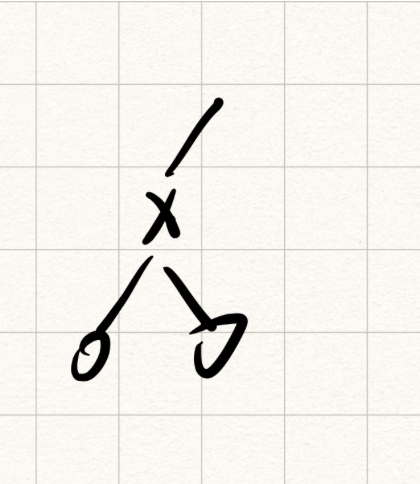
特殊的是，如果当前节点不是整个连通图的根节点，那需要给数量+1，因为它和父节点也是连通的，即下方的x，删掉x后，会形成3的分量

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod7 1000000007
#define mod9 998244353
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k;

int tot;
int head[MAX];
struct ran{
    int to, nex;
}tr[MAX];
inline void add(int u, int v){
    tr[++tot].to = v;
    tr[tot].nex = head[u];
    head[u] = tot;
}

int tmd;
int dfn[MAX], low[MAX];
int ans;
void tarjan(int u, int root){
    int num = 0;
    dfn[u] = low[u] = ++tmd;
    int sz = 0;
    for(int i = head[u]; i; i = tr[i].nex){
        int v = tr[i].to;
        ++sz;
        if(!dfn[v]){
            tarjan(v, root);
            low[u] = min(low[u], low[v]);
            if(low[v] >= dfn[u]){
                ++num;
            }
        }
        else{
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(u != root)++num;
    ans = max(ans, num);
}


void work(){
    while (cin >> n >> m && n + m) {
        mem(head, 0);tot = ans = tmd = 0;
        mem(dfn, 0);mem(low, 0);
        for(int i = 1, a, b; i <= m; ++i){
            cin >> a >> b;
            ++a;++b;
            add(a, b);add(b, a);
        }
        int cnt = 0;
        for(int i = 1; i <= n; ++i){
            if(!dfn[i]){
//                cout << i << endl;
                ++cnt;
                tarjan(i, i);
            }
        }
//        cout << cnt << ' ' << ans << endl;
        cout << cnt + ans - 1 << endl;
    }
}


int main(){
    io;
    work();
    return 0;
}