有依赖的背包问题

题目描述：

n个物品，容量为m,物品之间有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大

求最大价值

思路：

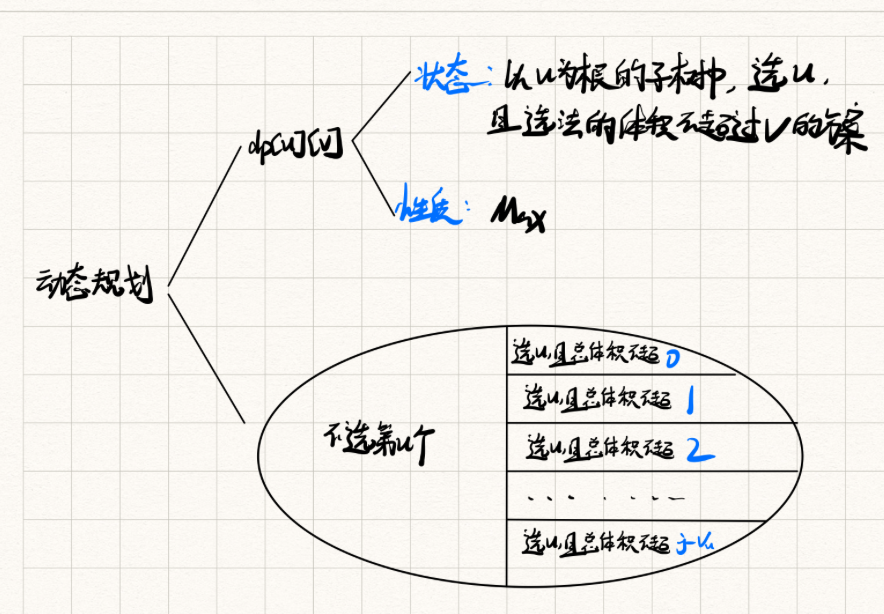
如果考虑每个子树中选哪些点，复杂度就是指数级别的，所以我们需要换一种分类方式，可以发现总体积很小，就100，可以考虑按背包的方式来定义，dp[u][v]表示以u为根的子树中，选u，且选择的体积不超过v的方案中的最大价值

对于u的每个子树v，我们可以枚举该子树v用的体积来更新u的值，因为分给子树体积v是不同的，就类似于分组背包的同一个组的物品，所以，第一维枚举体积，第二维枚举组内选法，也就是分给改子数v的体积

 

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 1000000007
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k;
int root;
int val[105], co[105];
vector<int>tr[105];
int dp[105][105];

void dfs(int u){
    for(int i = co[u]; i <= m; ++i)dp[u][i] = val[u];
    for(auto v : tr[u]){
        dfs(v);
        for(int j = m; j >= co[u]; --j){
            for(int k = 0; k <= j - co[u]; ++k){
                dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[v][k]);
            }
        }
    }
}

void work(){
    cin >> n >> m;
    for(int u = 1, v; u <= n; ++u){
        cin >> co[u] >> val[u] >> v;
        if(v == -1){
            root = u;continue;
        }
        tr[v].push_back(u);
    }
    dfs(root);
    cout << dp[root][m] << endl;
}


int main(){
    io;
    work();
    return 0;
}