最长公共上升子序列

题目描述：

给两个数组a和b

问两个序列的最长的公共上升子序列的长度

思路：

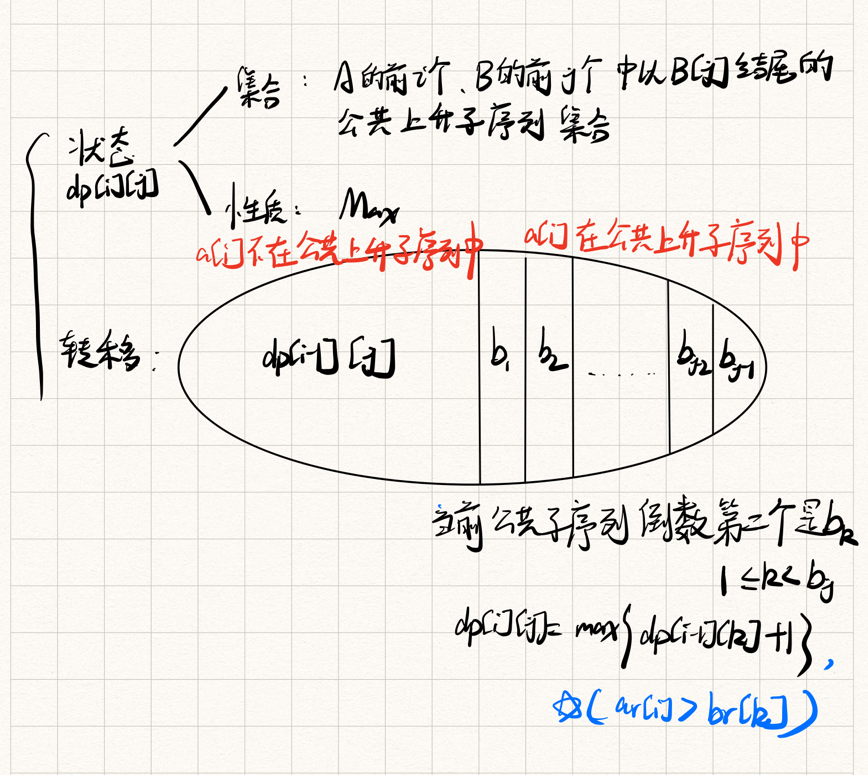
状态：dp[i][j]表示a数组的前i个，b数组的前j个中以br[j]为结尾的公共上升子序列的最大长度

转移方程可以将最长公共子序列和最长上升子序列结合起来思考

先思考最长公共子序列，也就是分成a[i]是否在公共上升子序列里，如果不再，则dp[i][j]=dp[i-1][j]，在的话，需要进行细分，按照最长上升子序列来进行细分，因为a[i]在当前公共上升子序列里，所以需要去找倒数第二个在当前公共上升子序列里面的点，也就是从1到j-1里面找a[i]>b[k]的点，他们有资格成为倒数第二个的点，计算最大值即可

for(int j = 1; j <= n; ++j){
         dp[i][j] = dp[i - 1][j];
         if(ar[i] == br[j]){
             dp[i][j] = max(dp[i][j], 1);
             for(int k = 1; k < j; ++k){
                 if(ar[i] > br[k]){
                     dp[i][j] = max(dp[i][j], dp[i - 1][k] + 1);
                 }
             }
         }
     }
 }

但是这样会TLE，得想办法优化

我们可以发现,每次找的都是1到j-1中的最大值，那就相当于是一个最大前缀，我们可以用一个变量记录下来这个最大值

for(int i = 1; i <= n; ++i){
     int maxn = 1;
     for(int j = 1; j <= n; ++j){
         dp[i][j] = dp[i - 1][j];
         if(ar[i] == br[j])dp[i][j] = max(dp[i][j], maxn);
         if(ar[i] > br[j])maxn = max(maxn, dp[i - 1][j] + 1);
     }
 }

 

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 1000000007
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)

typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k;
int ar[MAX];
int br[MAX];
int dp[3005][3005];

void work(){
    cin >> n;
    for(int i = 1; i <= n; ++i)cin >> ar[i];
    for(int i = 1; i <= n; ++i)cin >> br[i];
    int ans = 0;
    for(int i = 1; i <= n; ++i){
        int maxn = 1;
        for(int j = 1; j <= n; ++j){
            dp[i][j] = dp[i - 1][j];
            if(ar[i] == br[j])dp[i][j] = max(dp[i][j], maxn);
            if(ar[i] > br[j])maxn = max(maxn, dp[i - 1][j] + 1);
        }
    }
    for(int i = 1; i <= n; ++i)ans = max(ans, dp[n][i]);
    cout << ans << endl;
}


int main(){
    io;
    work();
    return 0;
}