并查集
简介:
最简洁而优雅的树形数据结构之一(没有之一
用于处理一些不交集(即一系列没有重复元素的集合)的合并及查询问题
支持两种操作:
- 查找:确定某个元素处于哪个子集
- 合并:将两个子集合并成一个集合
为什么并查集是树形结构?
因为并查集处理的是集合问题,但是对于一个元素x,你怎么知道x在哪个集合?这是不好确定的,那解决办法就是给每个集合引入一个特殊元素,用这个特殊元素来代表这个集合,然后再想办法将集合的每个元素都和这个特殊元素产生联系,这样就可以知道x是在哪个集合了。那有什么数据结构不仅可以将一堆数字联系起来,还可以有一个特殊的元素呢?那肯定是树了,树根就是那个特殊元素,而树的每个元素都绝对可以到达根,只需要一步步向上跑就行。所以树根就是外界识别这个集合的唯一标识!!!
问题引人
快过年了,强盗们也开始为年终奖“努力奋斗”了。强盗们有不同的团伙,警察叔叔想弄清楚到底有多少个强盗团伙,他手中收集到一些线索,让你帮忙分析一下。
注意,强盗的强盗也是同伙
我们先引入一个数组fa[i],表示 i 的上级是 fa[i], 初始化都为 fa[i] = i,即fa[i]是点 i 的父亲节点。
(这是对树形结构建图时常用的方法
void init(){
for(int i = 1; i <= n; ++i)fa[i] = i;
}
定义一个找根节点的函数–getfa()函数,用于找某个犯罪分子的代表首领(即根节点),这个函数可以写成一个递归的过程,x去找x的上级,x的上级再去找x的上级的上级,x的上级的上级再去找x的上级的上级的上级,由于根节点的父亲节点是自己,所以遇到fa[i] = i的情况就说明找到了根节点,此时就返回下标,这个下标就是x的根节点。
int getfa(int x){
if(x == fa[x])return x;//如果x的上级是他自己,说明x的唯一标识就行自己
else return getfa(fa[x]);//否则就是去找他上级的根
}
此外,我们还需要一个合并函数–emerge()函数,用于将两个犯罪团队进行合并,成为一个新的犯罪团队,也就是将两棵树合并成一棵树,而两个团队都有各自的代表首领,这是外界识别这个两个集合的唯一标识,我们只需要将这两个唯一的标识变成一个即可,也就是让其中一个代表元素的父节点变成另一个代表元素
void emerge(int x, int y){
int xx = getfa(x);//找x的根
int yy = getfa(y);//找y的根
fa[xx] = yy;//yy成为xx的父节点,yy成为新的集合的根结点
}
实操演练
书接上回
现在一共有9个强盗,1号与2号是同伙。3号与4号是同伙,5号与2号是同伙,4号与6号是同伙,2号与6号是同伙,8号与7号是同伙,9号与7号是同伙,1号与6号是同伙。
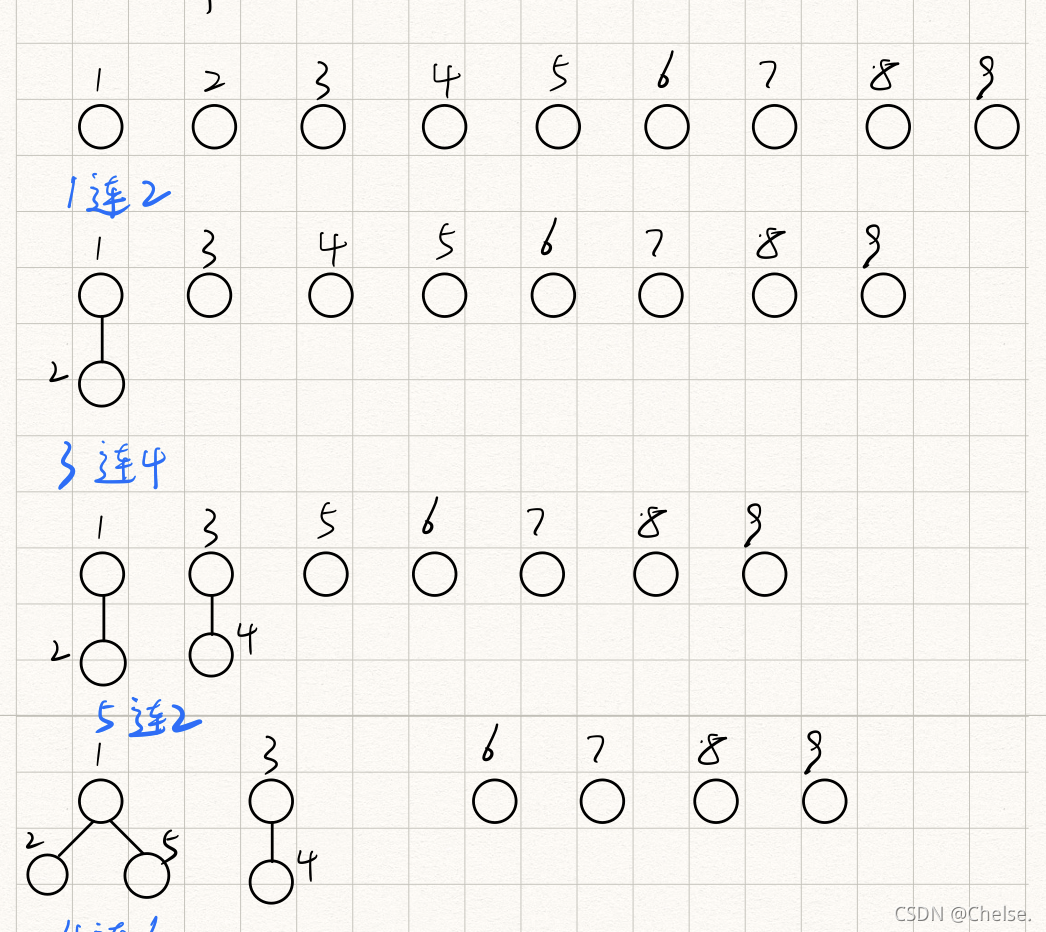
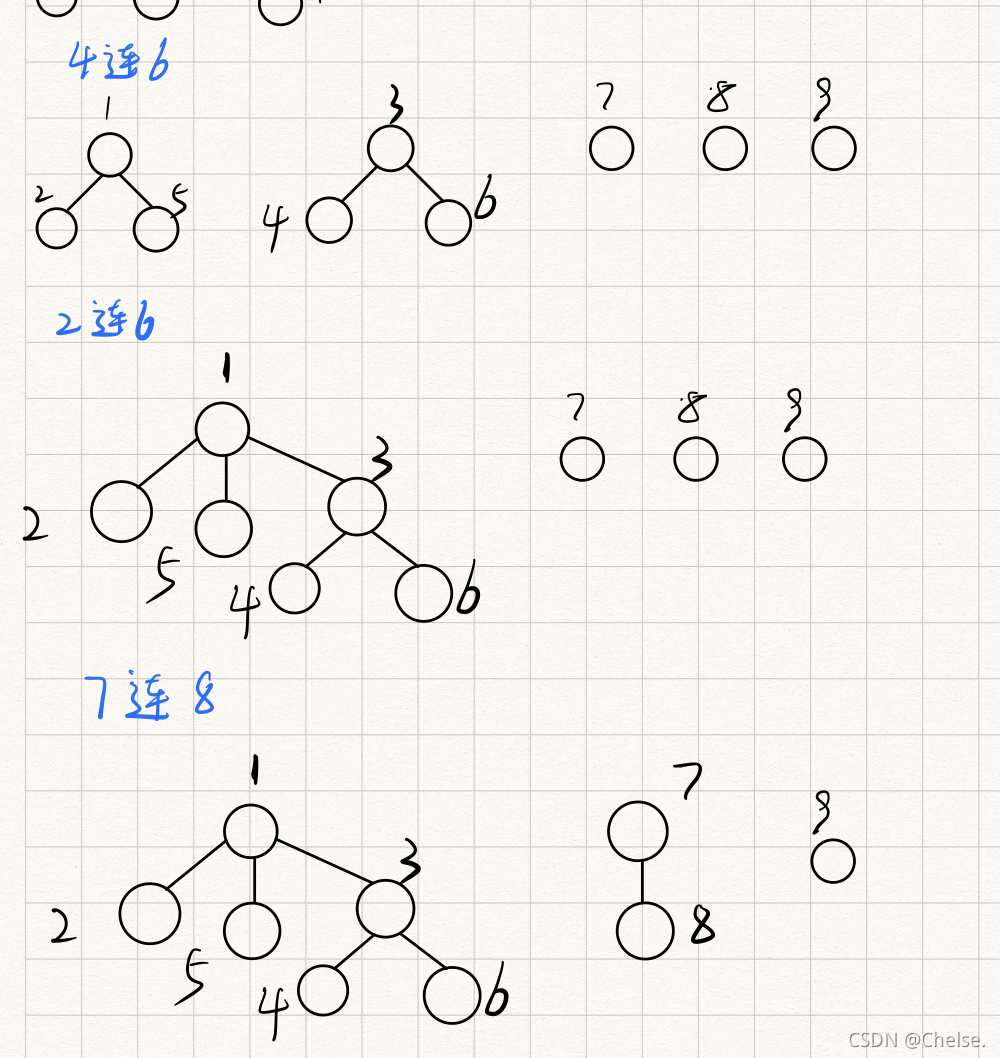
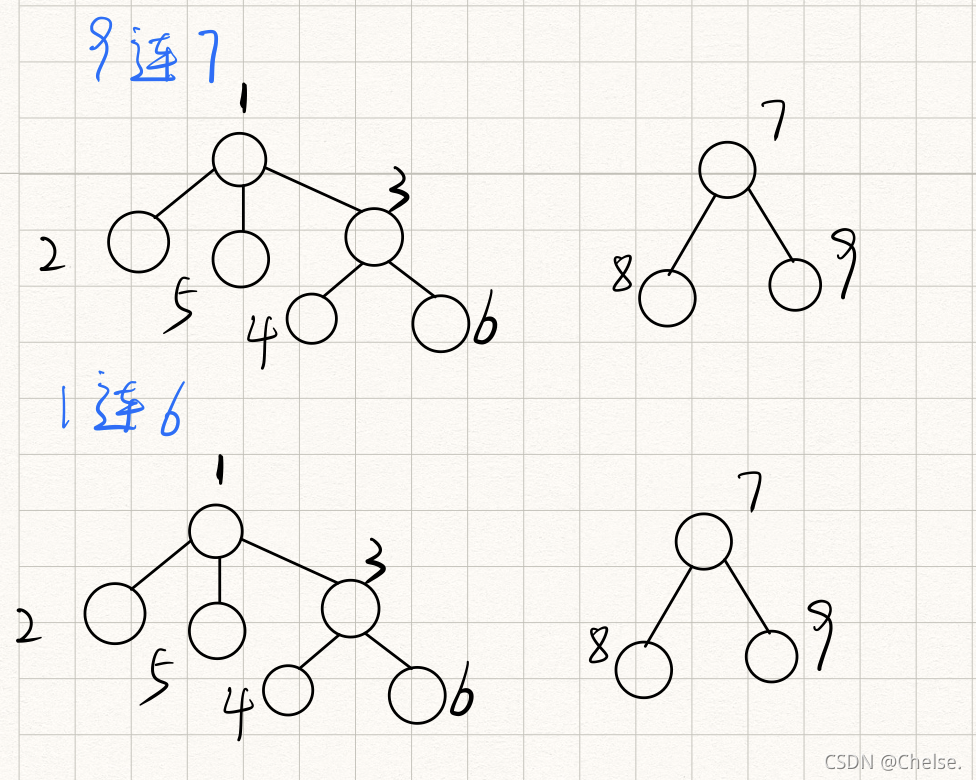
优化
路径压缩
分析一下可以发现,每个罪犯的上级不一定是这个集合的首领,所以getfa()会花费很多时间去找根节点,但是如果我们让能让集合的每个点都直接连到根结点就好了,那getfa函数就可以减少很多时间开销,方法就是在getfa()里面加一句话,也就是fa[x] = getfa[x]
int getfa(int x){
if(x == fa[x])return x;
else {
int p = getfa(fa[x]);//找到x的首领
fa[x] = p;//将x的fa变成x
return p;//返回首领
}
}
注意⚠️:只有进行getfa(x)时才会进行路径压缩,而且压缩的只是x到根结点之间的所有的点,在x下面的点那些是不会进行更新的
按秩合并
不使用路径压缩时,emerge函数在合并的过程中是随便将一个汇入另一个集合去,但是在某些极端情况会导致getfa函数特别慢,比如可能会形成一条链,这样每次去getfa都会花费很多的时间。分析一下,一棵树,从任意一个叶子结点向上递归找根节点的时间花费是log(n),n指的是树的深度,所以我们在合并的时候尽量不要去增加树的深度,也就是将深度小的接到深度大的树上去
这就需要一个数组 rk[i] 来记录 i 点的子树的深度,合并的时候比较两个集合的根结点的rk值来更新,初始化都为0
int rk[MAX];
inline void emerge(int x, int y){
int xx = getfa(x), yy = getfa(y);//xx是x的根结点,yy是y的根结点
if(xx == yy)return;//如果在同一个集合就返回就行
if(rk[xx] < rk[yy])fa[xx] = yy;//如果xx的子树的深度小于yy的,就把yy当作新的集合的根结点,把xx的集合汇入yy集合中
else {
fa[yy] = xx;//yy的子树深度小就相反
if(rk[xx] == rk[yy])++rk[xx];//深度相同的时候就更新rk值,因为此时必然会使其中一个的深度加1
}
}
注意,按秩合并(按树深)不可以和路径压缩同时使用,因为路径压缩的过程中可能会改变树深!!!如果非得要路径压缩和按秩合并一起用,那就用树的重量(即节点的总数量)来代替树深,因为路径压缩后根的重量不变
通常来说用路径压缩就行了,没必要写什么按秩合并
优美的并查集代码
int getfa(int x){
return x == fa[x] ? x : fa[x] = getfa(fa[x]);
}
inline void emerge(int x, int y){
fa[getfa(x)] = getfa(y);
}
void init(){//初始化很重要,不然会寄
for(int i = 1; i <= n; ++i)fa[i] = i;
}
时间复杂度
| 优化 | 平均复杂度 | 最坏时间复杂度 |
|---|---|---|
| 无优化 | O(logn) | O(n) |
| 路径压缩 | O(α(n)) | O(logn) |
| 按秩合并 | O(logn) | O(logn) |
这里 α 表示阿克曼函数的反函数,在宇宙可观测的 n 内(例如宇宙中包含的粒子总数),α(n) 不会超过 5。
应用1:简单板子题
题目描述:
n个人,m条信息,每条信息有x和y两个数,表示x和y属于同一个集合,问有多少个集合
思路:
板子题,并查集合并完统计一下fa[x] = x的数量即可
应用2:判联通图、统计联通图的数量
并查集还有个非常好用的地方就是判联通,一般都是给你的图,根据题目要求去emerge对应的点就行,最后根据getfa(x)与x的关系之类的就可以知道有多少个联通块,每个联通块的大小是多少等等
但是可能需要自己将去抽象出来合并用的点
K – Oil Deposits
代码样例
/*
Work by: Chelsea
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
//#include<unordered_map>
using namespace std;
//#pragma GCC optimize("Ofast")
//#pragma GCC target("fma,sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native")
//#pragma GCC optimize("unroll-loops")
#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define NMAX 1000 + 50
#define ls p<<1
#define rs p<<1|1
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sz(s) (int)(s).size()
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define sl(n) scanf("%lld",&n)
#define sll(n,m) scanf("%lld %lld",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define slll(n,m,z) scanf("%lld %lld %lld",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define m_p(a,b) make_pair(a, b)
typedef long long ll;
typedef pair <int,int> pii;
typedef unsigned long long ull;
//不开longlong见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
//不改范围见祖宗!!!
#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
int a, b, c;
string s, t;
char tr[105][105];
int fa[MAX];
int dx[] = {1, 0, -1, 0, 1, -1, 1, -1};
int dy[] = {0, 1, 0, -1, -1, 1, 1, -1};
inline void init(){
for(int i = 1; i <= n * m; ++i)fa[i] = i;
}
inline int getnum(int x, int y){
return (x - 1) * m + y;
}
bool judge(int x, int y){
if(x > n || x < 1 || y > m || y < 1)return false;
if(tr[x][y] == '*')return false;
return true;
}
inline int getfa(int x){
return x == fa[x] ? x : (fa[x] = getfa(fa[x]));
}
inline void emerge(int x, int y){
fa[getfa(x)] = getfa(y);
}
void work(){
while (cin>>n>>m && (n + m)) {
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
cin>>tr[i][j];
}
}
init();
for(int x = 1; x <= n; ++x){
for(int y = 1; y <= m; ++y){
if(tr[x][y] == '*')continue;
for(int k = 0; k < 8; ++k){
int xx = x + dx[k];
int yy = y + dy[k];
if(!judge(xx, yy))continue;
int u = getnum(x, y);
int v = getnum(xx, yy);
emerge(u, v);
}
}
}
int ans = 0;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
if(tr[i][j] == '@' && fa[getnum(i, j)] == getnum(i, j))++ans;
}
}
cout<<ans<<endl;
}
}
int main(){
io;
// int tt;cin>>tt;
// for(int _t = 1; _t <= tt; ++_t){
// printf("Case #%d: ", _t);
work();
// }
return 0;
}
应用3:最小生成树之Kruskal算法
本质就是贪心+并查集判断
将权值从小到大排个序,每条边都取出来判断该边的x和y是不是合并过了,没有就说明该边可以连,就emerge一下,同时更新答案
种类并查集
简介
种类并查集就是为了解决一些敌人的敌人是朋友的问题,维护的是一种循环对称的关系,他的作用就是不让两个有敌对关系的人在同一个队伍
一般是用于多种关系的题目中
比如一道经典的种类并查集:1078.食物链
题目描述:
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。 你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
思路:
两种关系,一种是x吃y,另一种是x和y是同类
三类动物,所以x就有三种可能,所以开三倍数组
1到n,表示是动物A,n+1到2 * n表示是动物B,2 * n + 1到3 * n表示是动物C
当给出的条件是x和y是同类的时候,我们就emerge(x, y),emerge(x + n, y + n),emerge(x + 2 * n, y + 2 * n),因为x和y是同类,但是并不知道是他们到底是哪个动物,所以就都合并一下
当给出的条件是x吃y时,因为是A吃B,B吃C,C吃A,ABC分别是1到n、n+1到2n、2n+1到3n,所以我们就emerge(x, y + n),emerge(x + n, y + 2 * n), emerge(x + 2 * n, y)就行
判断真假的时候
对于x和y是同类的时候,我们就判断x和y+n在不在一个集合,x和y+2n在不在一个集合,因为如果在一个集合就分别说明x吃y,y吃x,这都是不符合的
对于x吃y的时候,我们就判断x和y在不在一个集合,x和y + 2n在不在一个集合,因为如果在一个集合就分别说明x和y是同类,y吃x,这都是不符合的
/*
Work by: Chelsea
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
//#include<unordered_map>
using namespace std;
//#pragma GCC optimize("Ofast")
//#pragma GCC target("fma,sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native")
//#pragma GCC optimize("unroll-loops")
#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define NMAX 1000 + 50
#define ls p<<1
#define rs p<<1|1
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sz(s) (int)(s).size()
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define sl(n) scanf("%lld",&n)
#define sll(n,m) scanf("%lld %lld",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define slll(n,m,z) scanf("%lld %lld %lld",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define m_p(a,b) make_pair(a, b)
typedef long long ll;
typedef pair <int,int> pii;
typedef unsigned long long ull;
//不开longlong见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
//不改范围见祖宗!!!
#define MAX 300000 + 50
int n, m, k, op;
int x, y, z;
int a, b, c;
string s, t;
int fa[MAX];
int getfa(int x){
return x == fa[x] ? x : fa[x] = getfa(fa[x]);
}
inline void emerge(int x, int y){
fa[getfa(x)] = getfa(y);
}
void work(){
cin>>n>>m;
for(int i = 1; i <= 3 * n; ++i)fa[i] = i;
int ans = 0;
for(int i = 1; i <= m; ++i){
cin>>op>>x>>y;
if(x > n || y > n)++ans;
else{
if(op == 1){
if(getfa(x) == getfa(y + n) || getfa(x) == getfa(y + 2 * n)){
++ans;
continue;
}
emerge(x, y);
emerge(x + n, y + n);
emerge(x + 2 * n, y + 2 * n);
}
else{
if(getfa(x) == getfa(y) || getfa(x) == getfa(y + 2 * n)){
++ans;
continue;
}
emerge(x, y + n);
emerge(x + n, y + 2 * n);
emerge(x + 2 * n, y);
}
}
}
cout<<ans<<endl;
}
int main(){
io;
// int tt;cin>>tt;
// for(int _t = 1; _t <= tt; ++_t){
// printf("Case #%d: ", _t);
work();
// }
return 0;
}
