差分 – 前缀和
一维数组前缀和
为什么要学前缀和呢?学前缀和有什么用呢?
让我们先看一下1657题来感受一下前缀和之“神奇”
题意:
给你n个数,然后问你q次,每次询问1到p的所有数的算数和,最简单的想法是每次询问我写个for循环遍历一遍就完事了呗,但是很快的啊,一发TLE送你回家,这个时候前缀和就是一个很好的方法!
前缀和的思路:
就是for循环输入tr数组的时候,用另一个数组存下来前缀和,如下:
ar[i] = ar[i - 1] + tr[i];
具体代码如下:
#include<bits/stdc++.h>
using namespace std;
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
ll tr[1000005], ar[1000005];
int main()
{
ll n, m, k;
cin>>n>>m;
for(int i = 1; i <= n; i++)
{
cin>>tr[i];
ar[i] = ar[i - 1] + tr[i];
}
for(int i = 1; i <= m; i++)
{
cin>>k;
cout<<ar[k]<<'\n';
}
}
(提交的时候一定要记得开longlong,不然一发wa给你安排的明明白白的!!!
然后就是进阶版的前缀和,见1658题,再1657的基础上,这次是查找的一个给定区间内的数
思路:
用前缀和的差即可,ar[b] – ar[a]
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll tr[1000005], ar[1000005];//记得开ll
int main()
{
ll n, m, k, a;
scanf("%lld%lld",&n, &m);//最好用scanf,用cin时间就会慢很多
for(int i = 1; i <= n; i++)
{
scanf("%lld",&tr[i]);
ar[i] = ar[i - 1] + tr[i];//前缀和操作
}
for(int i = 1; i <= m; i++)
{
scanf("%lld%lld",&k, &a);
cout<<ar[a] - ar[k - 1]<<'\n';//要用后面的减前面的,不要搞混,而且是k-1
}
return 0;
}
二维数组的前缀和
二维数组和一维数组差不多,但是你得手推一下公式
先看简单一点的二维前缀和
题意:
给你n * m大小的二维数组,q次查询,每次查询都给你两个数x,y 要求输出(1,1)与(x, y)形成的矩形内所有的数的和(不会打求和的那个符号,只能换个方式描述了)
先观察一下,每次都是求从起点(1,1)开始的方阵,所以我们的递推关系中用到的也得是从(1,1)开始的方阵进行加减操作
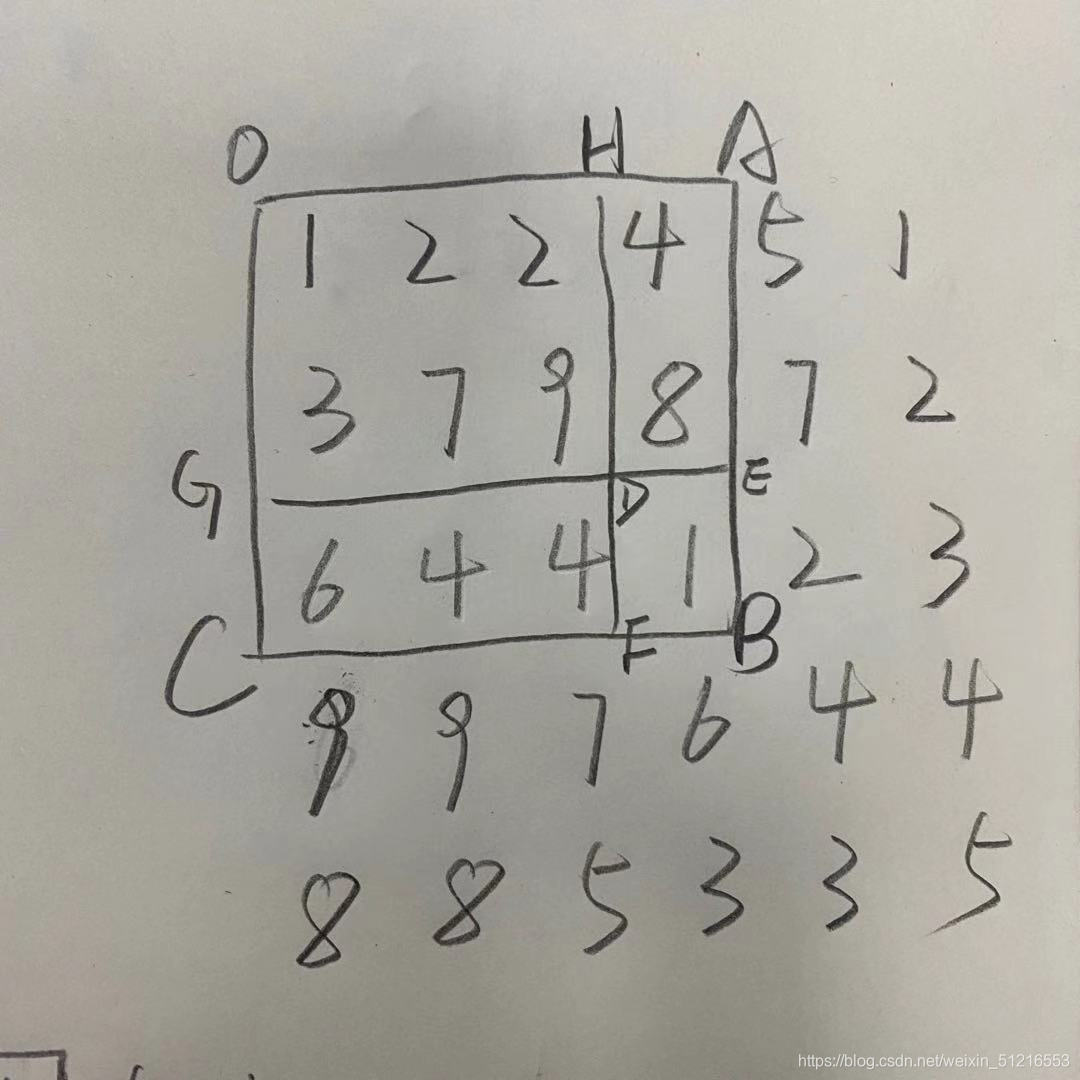
我们先看一个例子:求图中OABC内所有的数的和。
要求的是方阵OABC内所有数的和,通过观察可得OABC = OHFC + OGEA – OHDG + DEBF
然后其中的OHFC OGEA OHDG也是前缀和数组,求他们的方法同上,就进行了递推……
所以规律就出来了!
因为是二维数组,所以要写两层循环
for(int i = 1; i <= n; i++)
for(int j = 1; j<= m; j++)
sum[i][j] = sum[i - 1][j] + sum[i][j -1] - sum[i - 1][j - 1] + tr[i][j];
//sum数组是前缀和数组,tr数组是原二维数组
具体代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll tr[1005][1005], ar[1005][1005];
int main()
{
ll n, m, q, k, a;
scanf("%lld%lld%lld",&n, &m, &q);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
scanf("%lld",&tr[i][j]);
ar[i][j] = ar[i - 1][j] + ar[i][j - 1] - ar[i - 1][j - 1] + tr[i][j];
}
}
for(int i = 1; i <= q; i++)
{
scanf("%lld%lld",&k, &a);
cout<<ar[k][a]<<'\n';
}
return 0;
}
然后就是进阶版的1660
相比于1659,这次不是才从(1,1)开始,而是由输入决定
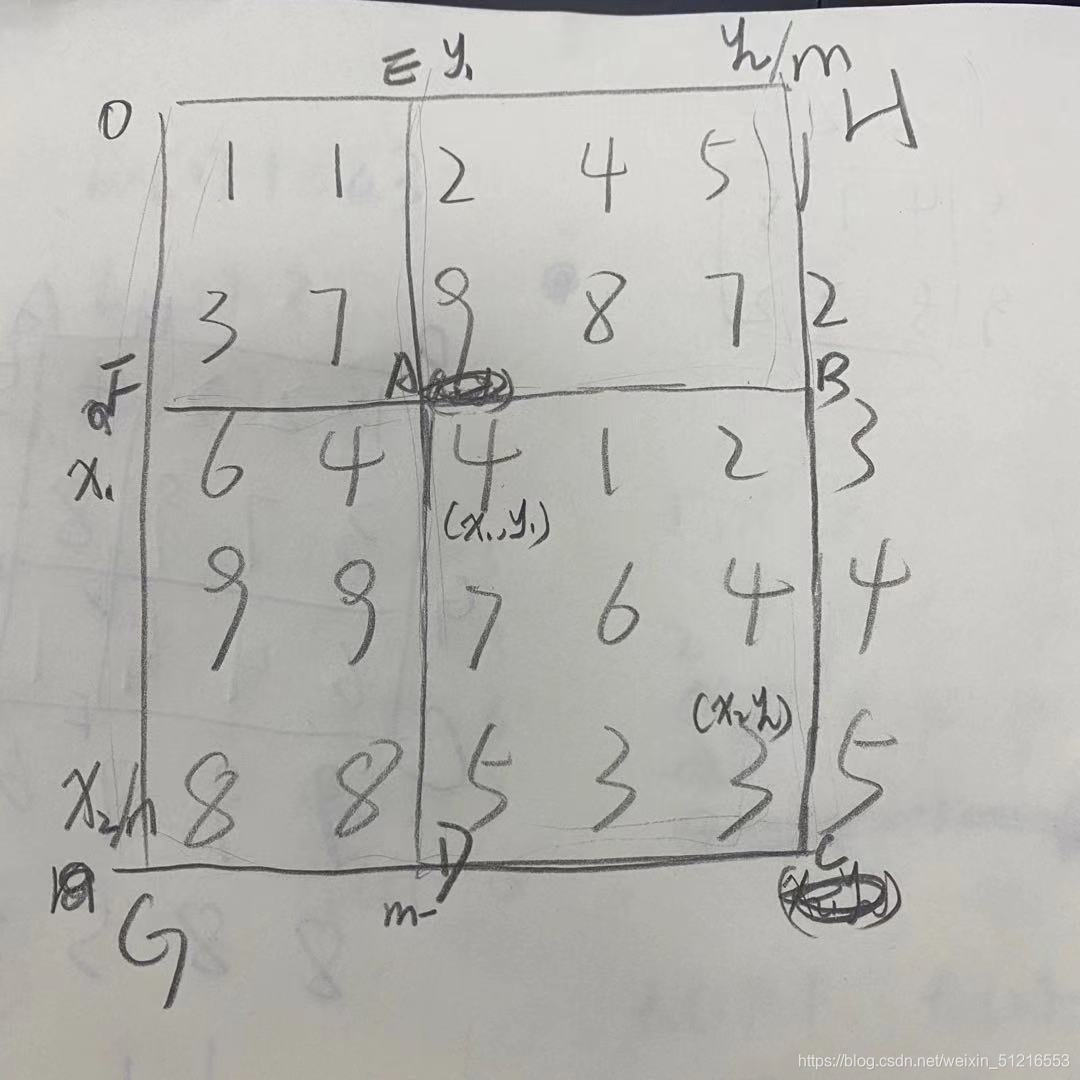
我们参考一维数组的前缀和,是通过sum[b] – sum[a – 1]来求,所以该进阶版二维数组的前缀和的道理也差不多,也是通过前缀和的加减来实现,而首当其冲的就是找到这个规律:假设我们要求ABCD内数的和,我们可以把转变一下,利用(1, 1)的前缀和来求,也就是ABCD = OGCH – OEAF – OFBH + OEAF
sum[x2][y2] + sum[x1 - 1][y1 - 1] - sum[x2][y2 -1] - sum[x1 - 1][y2]
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll tr[1005][1005], ar[1005][1005];
int main()
{
ll n, m, q, b, c, d, a;
scanf("%lld%lld%lld",&n, &m, &q);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
scanf("%lld",&tr[i][j]);
ar[i][j] = ar[i - 1][j] + ar[i][j - 1] - ar[i - 1][j - 1] + tr[i][j];//还是需要先求一下从(1,1)开始的前缀和
}
}
for(int i = 1; i <= q; i++)
{
scanf("%lld%lld%lld%lld",&x1, &y1, &x2, &y2);
cout<<ar[x2][y2] + ar[x1 - 1][y1 - 1] - ar[x2][y2 -1] - ar[x1 - 1][y2]<<'\n';
}
return 0;
}
前缀和的应用
主要解决连续子数组的问题,包括矩阵
1.子段求和,如上面的那四道题
2.问某些特定的连续的子数组的个数
主要思想是利用两层for循环,找到符合的条件(可以利用哈希表进行优化,但是我不会,手动狗头.jpg
3.和差分结合应用……
前缀和总结:
前缀和是一种重要的预处理,能大大降低查询的复杂度。一维前缀和比较简单,用于解决指定区间内值的和的问题。二维数组就需要找到递推关系来求解,并且要求(x1, y1)(x2,y2)形成的矩形内所有的数的和需要利用从(1,1)的前缀和之间的规律求解,递推关系和规律都是基于容斥原理的。
差分
差分与前缀和互逆,常与前缀和一起使用,求完差分后求其前缀和则可得到修改后的数据
题意:
给你一个数组,初始值都是0,进行q次操作,每次操作对给定区间的的所有数都进行加减运算,最后输出整个数组
思路:
如果直接暴力的话,每次修改的复杂度都是O(n),也是一发TLE让你怀疑人生,所有就有了差分的用武之地……
先创建一个差分数组tr,每次操作是对(l, r)区间加上c,就可以转换成对tr[l] += c, tr[r + 1] -= c,然后再对tr数组求一次前缀和,即可得到原来的数组。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
/*这个是快读,因为cin超时,再加上不喜欢打scanf,就直接CV快读挂板子,一提交能比别快十倍(手动狗头.jpg*/
inline int IntRead()
{
char ch = getchar();
int s = 0, w = 1;
while(ch < '0' || ch > '9')
{
if(ch == '-') w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
s = s * 10 + ch - '0',
ch = getchar();
}
return s * w;
}
ll tr[100005], ar[100005];//ar[]是最后求的前缀和数组,也就是最后输出的数组,tr[]是差分数组
int main()
{
ll n, m, a, b, c;
n = IntRead();
m = IntRead();
for(int i = 0; i < m; i++)
{
a = IntRead();
b = IntRead();
c = IntRead();
tr[a] += c;
tr[b + 1] -= c;//注意是b + 1
}
for(int i = 1; i <= n; i++)
{
ar[i] = ar[i - 1] + tr[i];//求前缀和
}
for(int i = 1; i <= n; i++)
{
if(i == 1)//控制空格的输出
cout<<ar[i];
else
cout<<' '<<ar[i];
}
cout<<endl;
return 0;
}
再来个进阶版的差分数组1662
这次在原来的基础上改了一下原数组的值,从0变成别的值而已,就在最后输出的时候加上即可
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll tr[100005], ar[100005], br[100005];//这次的tr数组是数组的初始值,ar是差分数组,br是前缀和数组
inline int IntRead()
{
char ch = getchar();
int s = 0, w = 1;
while(ch < '0' || ch > '9')
{
if(ch == '-') w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
s = s * 10 + ch - '0',
ch = getchar();
}
return s * w;
}
int main()
{
ll n, m, a, b, c;
n = IntRead();
m = IntRead();
for(int i = 1; i <= n; i++)
{
tr[i] = IntRead();
}
for(int i = 0; i < m; i++)
{
a = IntRead();
b = IntRead();
c = IntRead();
br[a] += c;
br[b + 1] -= c;
}
for(int i = 1; i <= n; i++)
{
ar[i] = ar[i - 1] + br[i];
if(i == 1)
cout<<ar[i] + tr[i];
else
cout<<' '<<ar[i] + tr[i];
}
cout<<endl;
return 0;
}
前缀和有二维的,差分自然也有(别的小朋友有的,你也得有!
题意:
给你一个n*m 大小的二维数组,初始都是0,进行q次操作,每次操作是对一个子数组的每个元素进行加减操作,最终输出整个数组
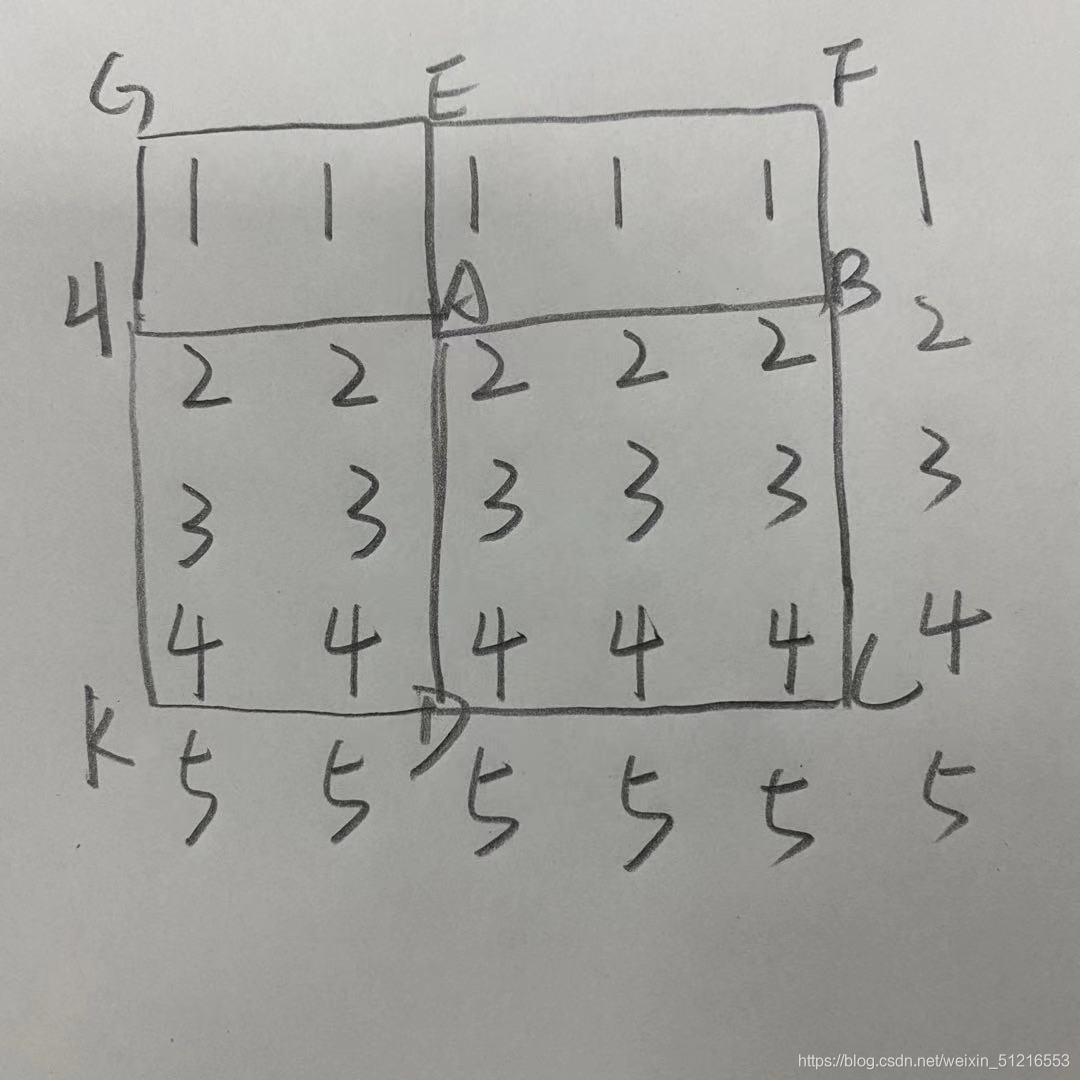
思路和一维的一样,让某个或某些差分数组的值加或减c,通过这些差分数组的改变,再利用前缀和,即可影响到所需的区间
ABCD = CFGK – GEDK – GHBF + AEGH
所以我们就让差分数组tr [x2] [y2] += a, tr[x2] [y1 – 1] -= a, tr[x1 – 1] [y2] -= a , tr[x1] [y1] += a
然后利用二维数组前缀和求解
#include<bits/stdc++.h>
using namespace std;
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
ll tr[1005][1005], ar[1005][1005];//tr是差分数组,ar是前缀和数组
int main()
{
ll n, m, q, x1, x2, y1, y2, c;
scanf("%lld%lld%lld",&n, &m, &q);
while(q--)
{
scanf("%lld%lld%lld%lld%lld",&x1, &y1, &x2, &y2, &c);
tr[x1][y1] += c;
tr[x1][y2 + 1] -= c;
tr[x2 + 1][y1] -= c;
tr[x2 + 1][y2 + 1] += c;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
ar[i][j] = ar[i - 1][j] + ar[i][j - 1] - ar[i - 1][j - 1] + tr[i][j];
if(j == 1)
cout<<ar[i][j];
else
cout<<' '<<ar[i][j];
}
cout<<'\n';
}
return 0;
}
1664进阶版的二维差分,就是先给二维数组赋值了,方法和上面一样,只不过最后要加上二维数组的原始值
#include<bits/stdc++.h>
using namespace std;
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;
inline int IntRead()
{
char ch = getchar();
int s = 0, w = 1;
while(ch < '0' || ch > '9')
{
if(ch == '-') w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
s = s * 10 + ch - '0',
ch = getchar();
}
return s * w;
}
ll tr[1005][1005], ar[1005][1005], br[1005][1005];//tr是差分数组,ar是前缀和数组
int main()
{
ll n, m, q, x1, x2, y1, y2, c;
n = IntRead();
m = IntRead();
q = IntRead();
//scanf("%lld%lld%lld",&n, &m, &q);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
br[i][j] = IntRead();
}
}
while(q--)
{
x1 = IntRead();
y1 = IntRead();
x2 = IntRead();
y2 = IntRead();
c = IntRead();
//scanf("%lld%lld%lld%lld%lld",&x1, &y1, &x2, &y2, &c);
tr[x1][y1] += c;
tr[x1][y2 + 1] -= c;
tr[x2 + 1][y1] -= c;
tr[x2 + 1][y2 + 1] += c;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
ar[i][j] = ar[i - 1][j] + ar[i][j - 1] - ar[i - 1][j - 1] + tr[i][j];
if(j == 1)
cout<<ar[i][j] + br[i][j];
else
cout<<' '<<ar[i][j] + br[i][j];
}
cout<<'\n';
}
return 0;
}
差分数组的应用
主要是可以快速处理区间加减操作,包括一维数组,二维数组,树等,节约时间
差分总结
差分数组主要维护的是两个相邻的数据之差,主要用来配合前缀和发挥作用的,对于区间的加减操作很好使,还可以结合树状数组等进行高级搭配
